三角函数y1=cosx/4与y2=sin6x/5的交点计算

1、两函数y1=cosx/4与y2=sin6x/5在同一坐标下的示意图:从图像看，交点在x轴上下方依次出现，由于三角函数的周期性，所以二者的交点有无数个。

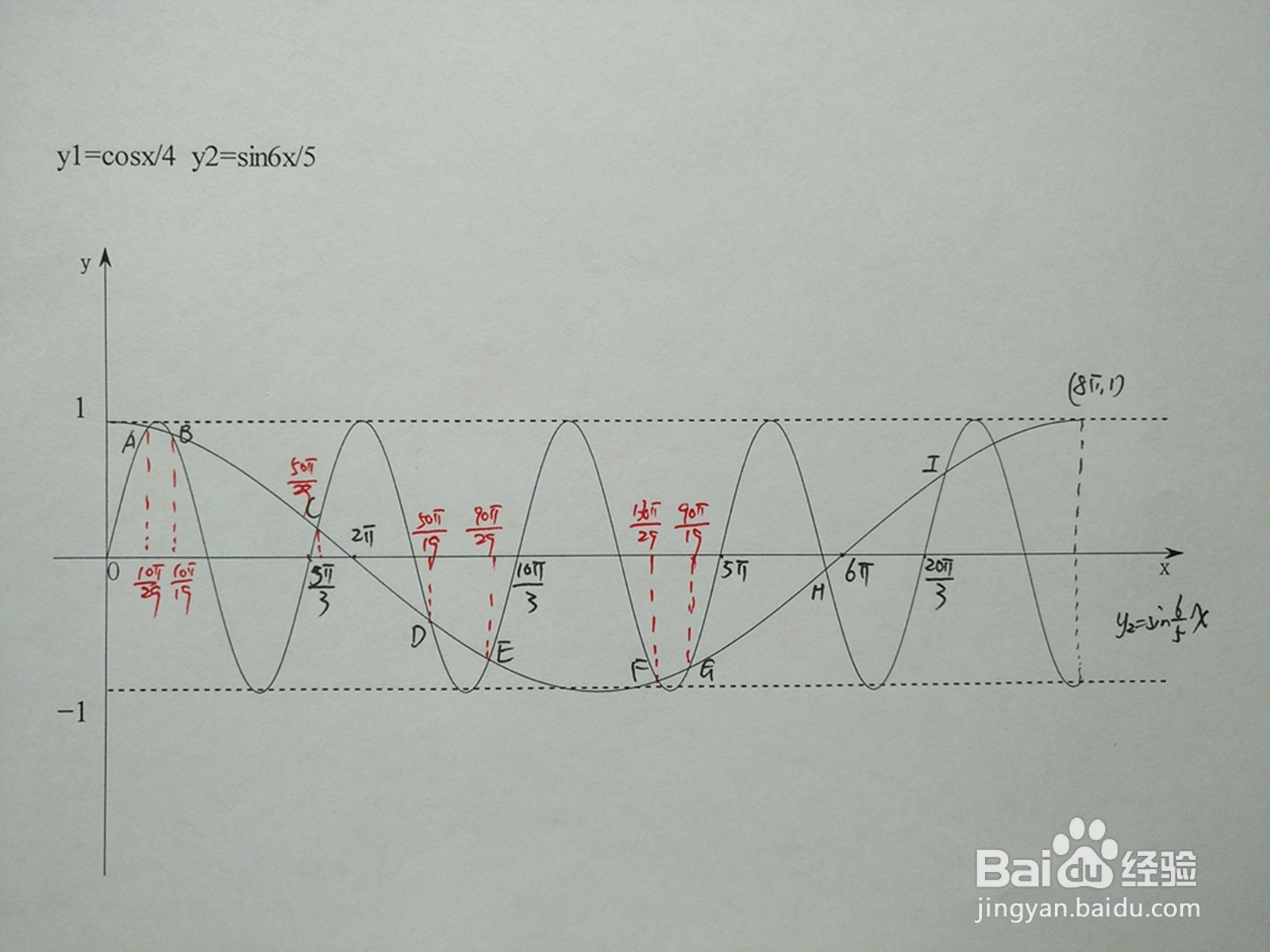
2、 三角函数：三角函数是数学中属于初等函数中的超越函数的函数。它尺攵跋赈们的本质是任何角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的。本文中y1=cosx/桃轾庾殇4为余弦三角函数，y2=sin6x/5为正弦三角函数。

3、交点通式，联立方程，用和差化积sinθ−s坡纠课柩inφ=2cos(θ+φ)/2sin(θ−φ)/2公式求y1=cosx/4与y2=sin6x/5交点。

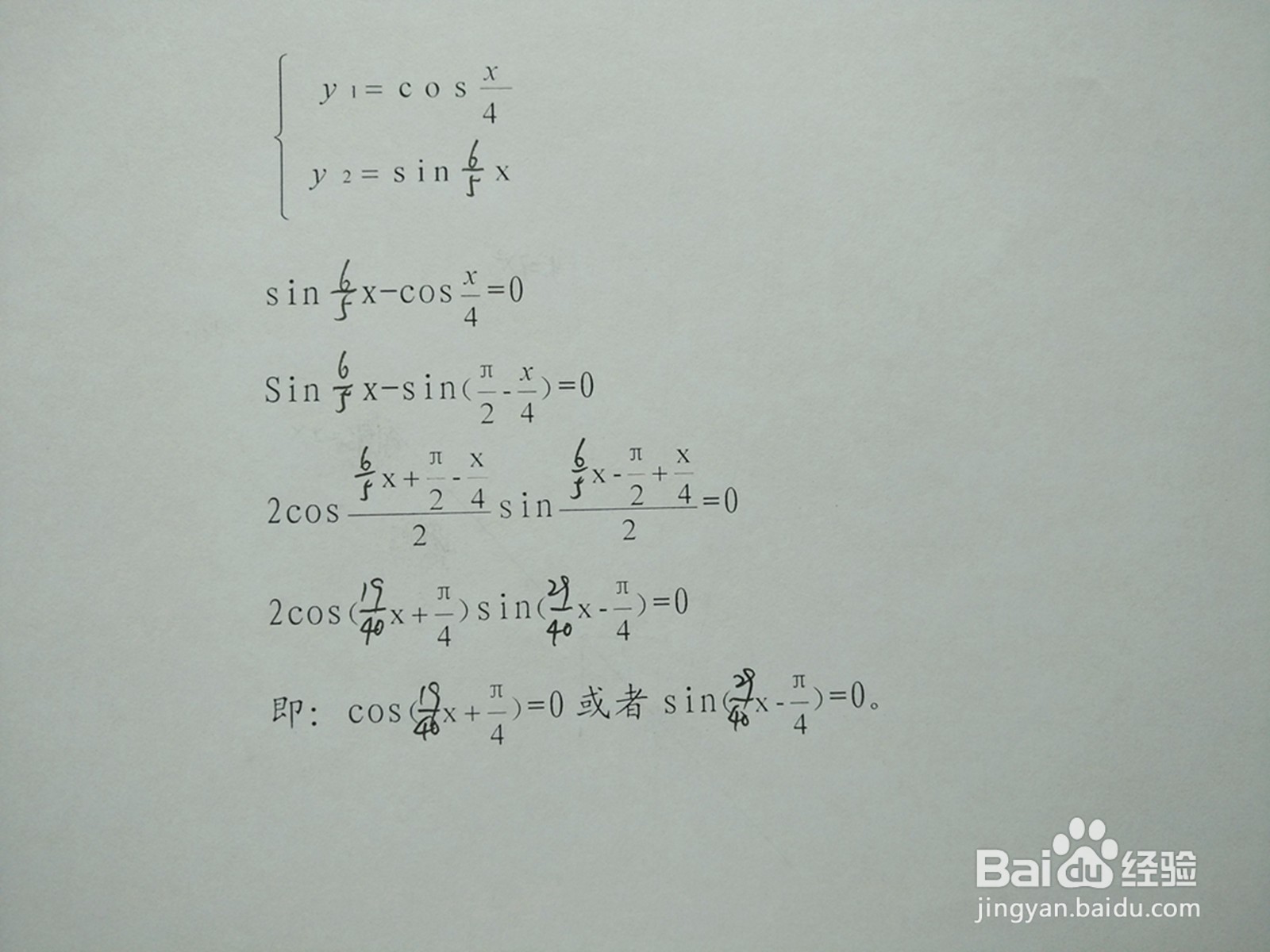
4、解析余弦函数y1=cosx/4与正弦函数y2=sin6x/5交点通式。

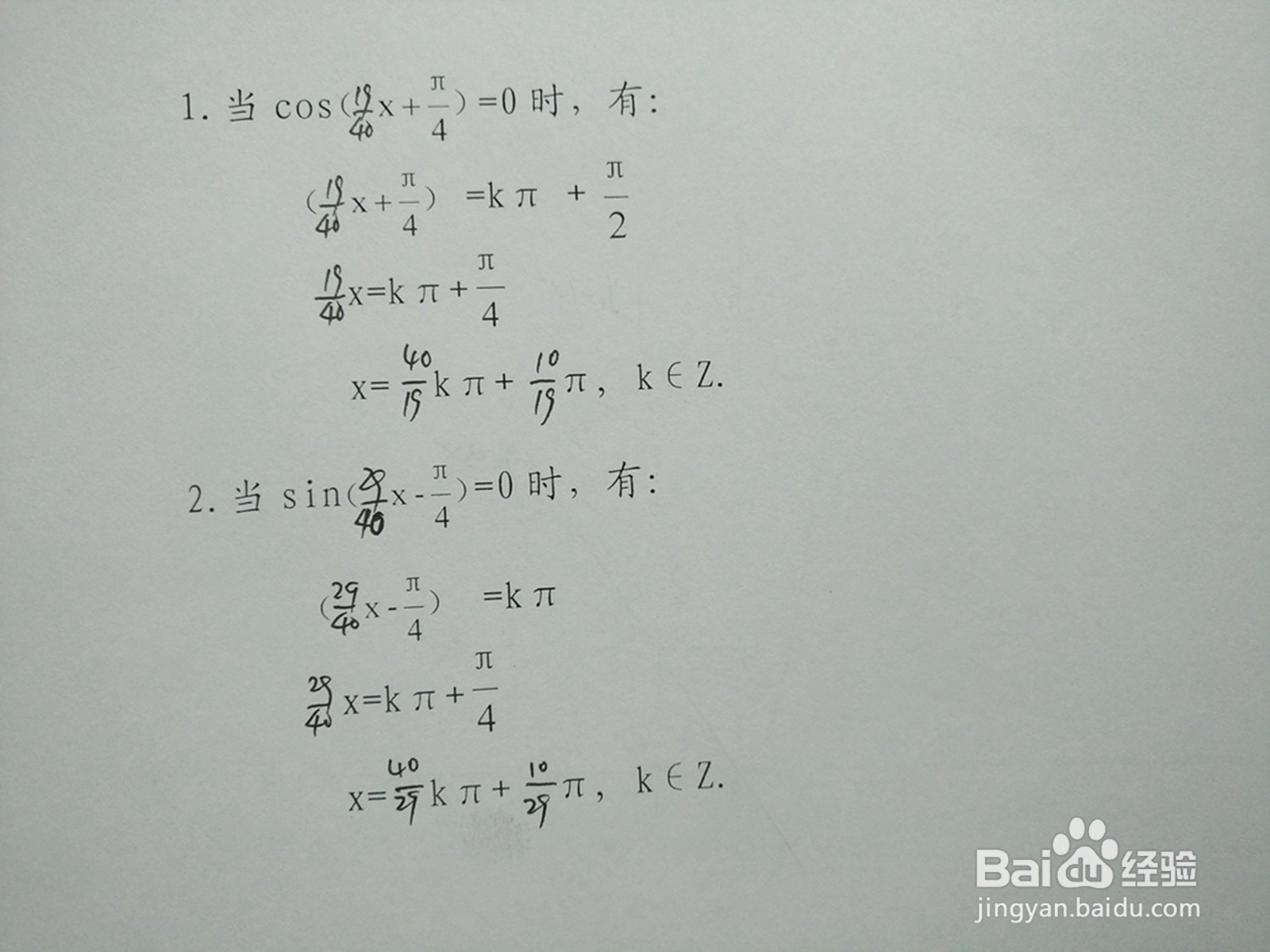
5、交点解析表，解析两函数y1=cosx/4与y2=sin6x/5部分交点横坐标，如下表。

6、函数交点，两函数y1=cosx/4与y2=sin6x/5在部分周期内，交点坐标如下：

7、余弦函数y1=cosx/4与和正弦函数y2=sin6x/5在部分周期上部分交点如下。