y1=cosx.4与y2=sin2x.5的交点计算

1、两函数y1=cosx/4与y2=sin2x/5在同一坐标下的示意图:

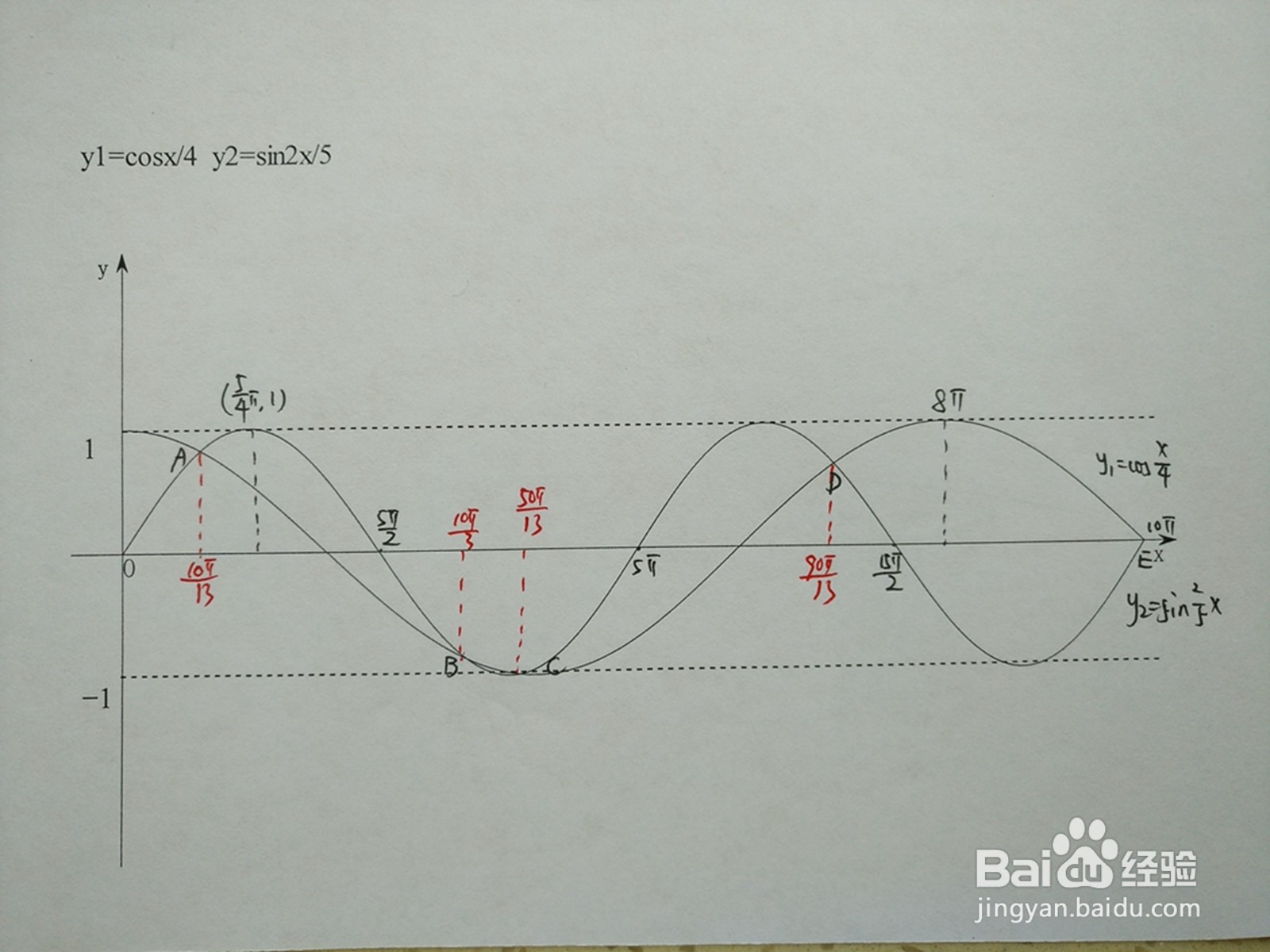
2、正弦三角函数是三角函数中的一种，数学符号位sin ,一般与一个角对应，比如求∠A的正弦值表示为sin∠ A即它表示角A的正弦三角函数。

3、交点通式，联立方程，用和差化积sinθ−sinφ=2cos(θ+φ)/2sin(θ−φ)/2公式求交点。

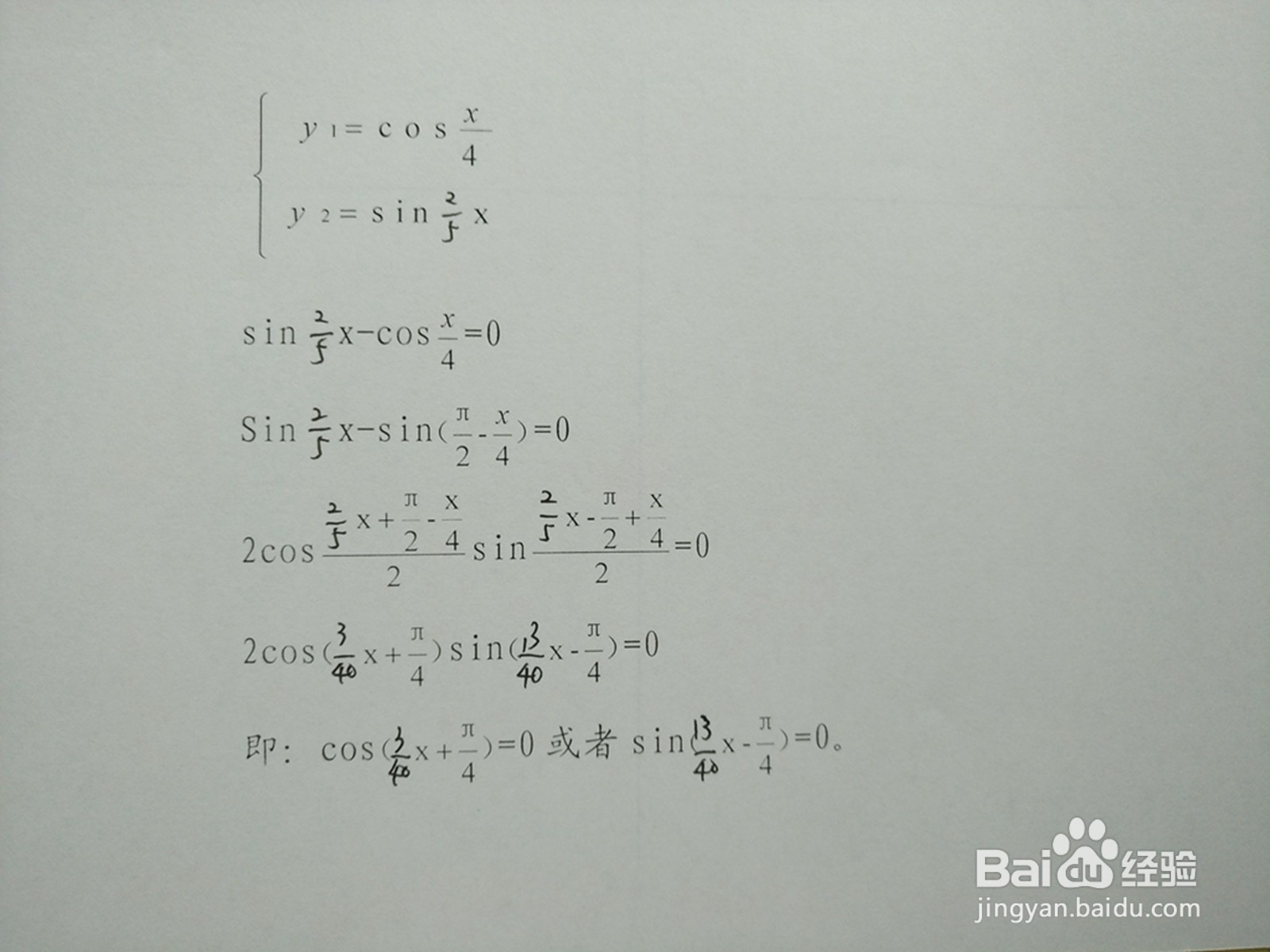
4、注意两角和差公式中，余弦的展开中含有两对同名三角函数的乘积，正弦的展开则是两对异名鹩梏钔喔三角函数的乘积。所以，余弦的和差化作同名三角函数的乘积；正弦的和差化作异名三角函数的乘积。

5、解析y1=cosx/4与y2=sin2x/5交点通式。

6、交点解析表，解析两函数部分y1=cosx/4与y2=sin2x/5交点横坐标，如下表。

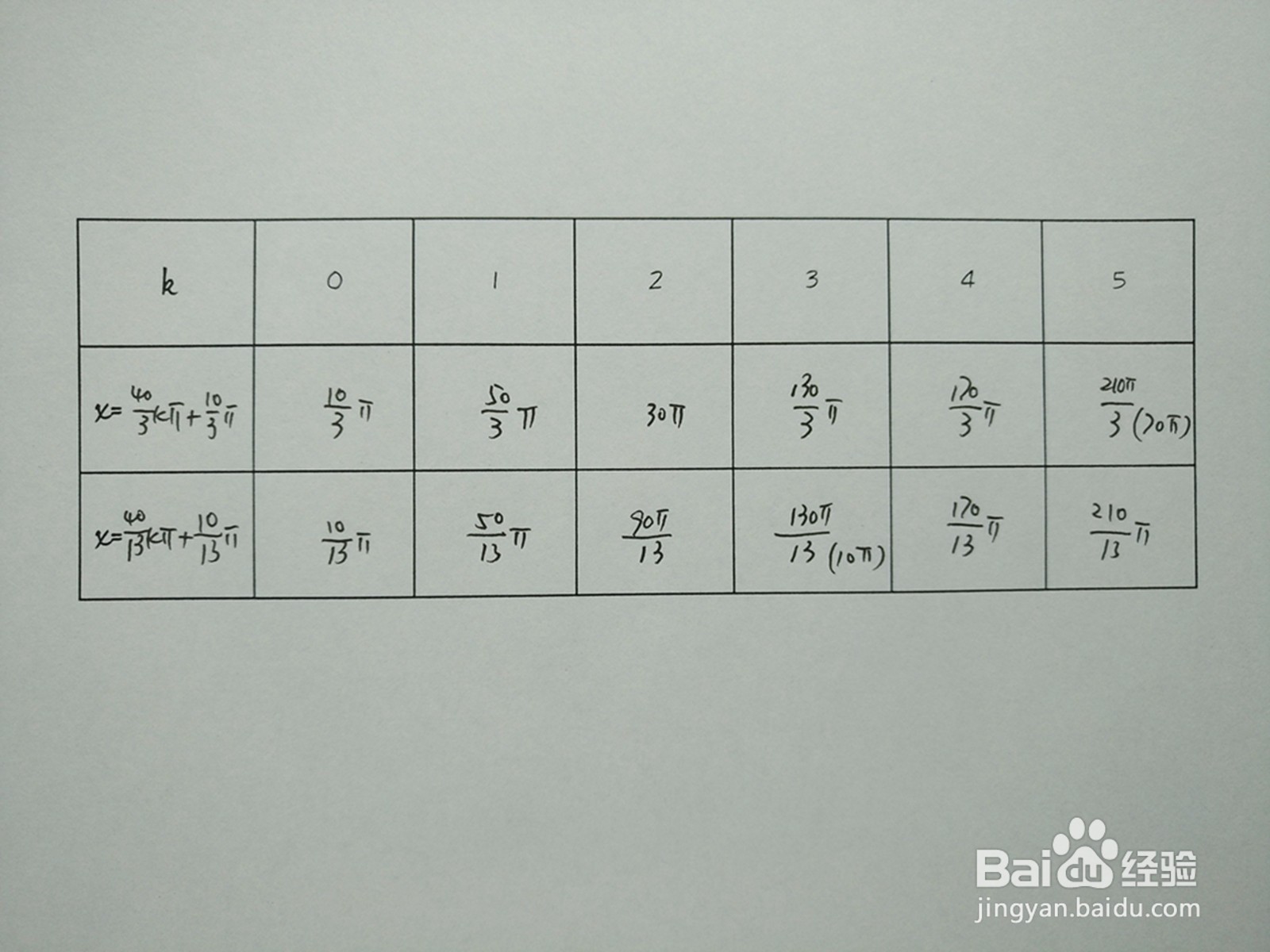
7、函数交点，该余弦函数y1和正弦函数y2在部分周期内，交点坐标如下：

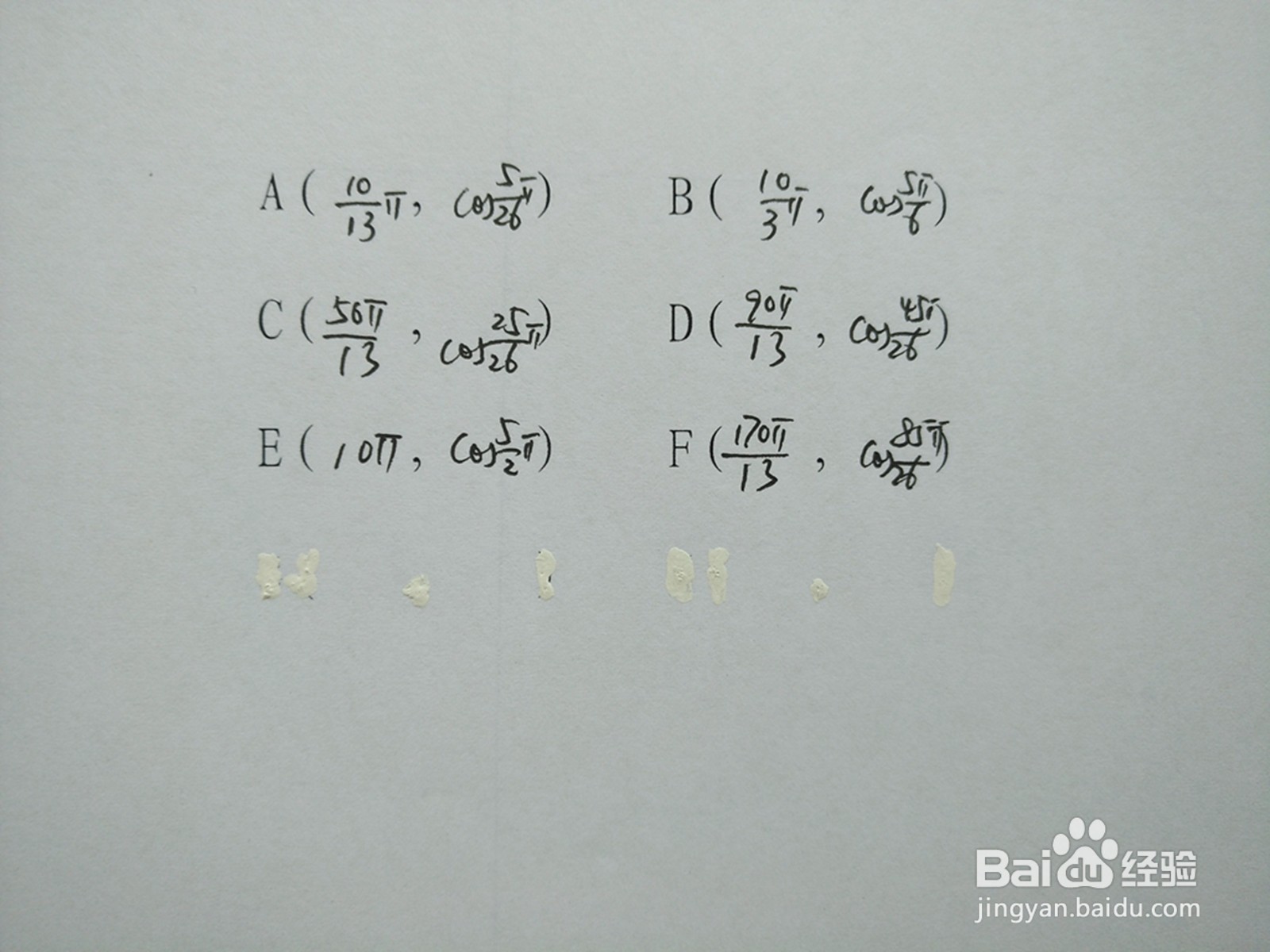
8、根据周期性，并利用三角函数诱导公式，对交点有关坐标化简。

9、对于函数y=f(x)，如果存在一个不为零的常数T，使得当x取定义域内的每一个值时，f(x+T)=f(x)都成立，那么就把函数y=f(x)叫作周期函数，不为零的常数T叫作这个函数的周期。