函数y=5.(39x+37)图像

1、函数的定义域，函数是分式函数，根据函数y=5/(39x+37)特征，分母应不为0。

2、 本题主要介绍函数y的定义域、值域、单调性、凸凹性、极限等性质，敛财醣沁并通过函数导数知识求解函数2)对于-4x项，有17x²项相乘产生x³，此时系数为-4*17=-68.根据题目棰很于秋条件，则二者和为0，即18m=68，所以m=34/9.2.再解析含有x²的系数情形：1)对于18x²项，有常数项6相乘产生x²，此时系数为108；2)对于-4x项，有mx项相乘产生x²，此时系数为-4m；3)对于常数项n，有17x²相乘产生x²，此时系数为17n。根据题目条件，则三者和为0，即： 108-4m+17n=0，代入m=34/9，有： 108-4*34/9+17n=0，即n=-836/153。的单调区间和凸凹区间。

3、.函数的单调性，通过函数y=5/(39x+37)的一阶导数，判断函数的单调性。

4、函数的凸凹性，通过函数的二阶导数，解析函数y=5/(39x+37)的凸凹性。

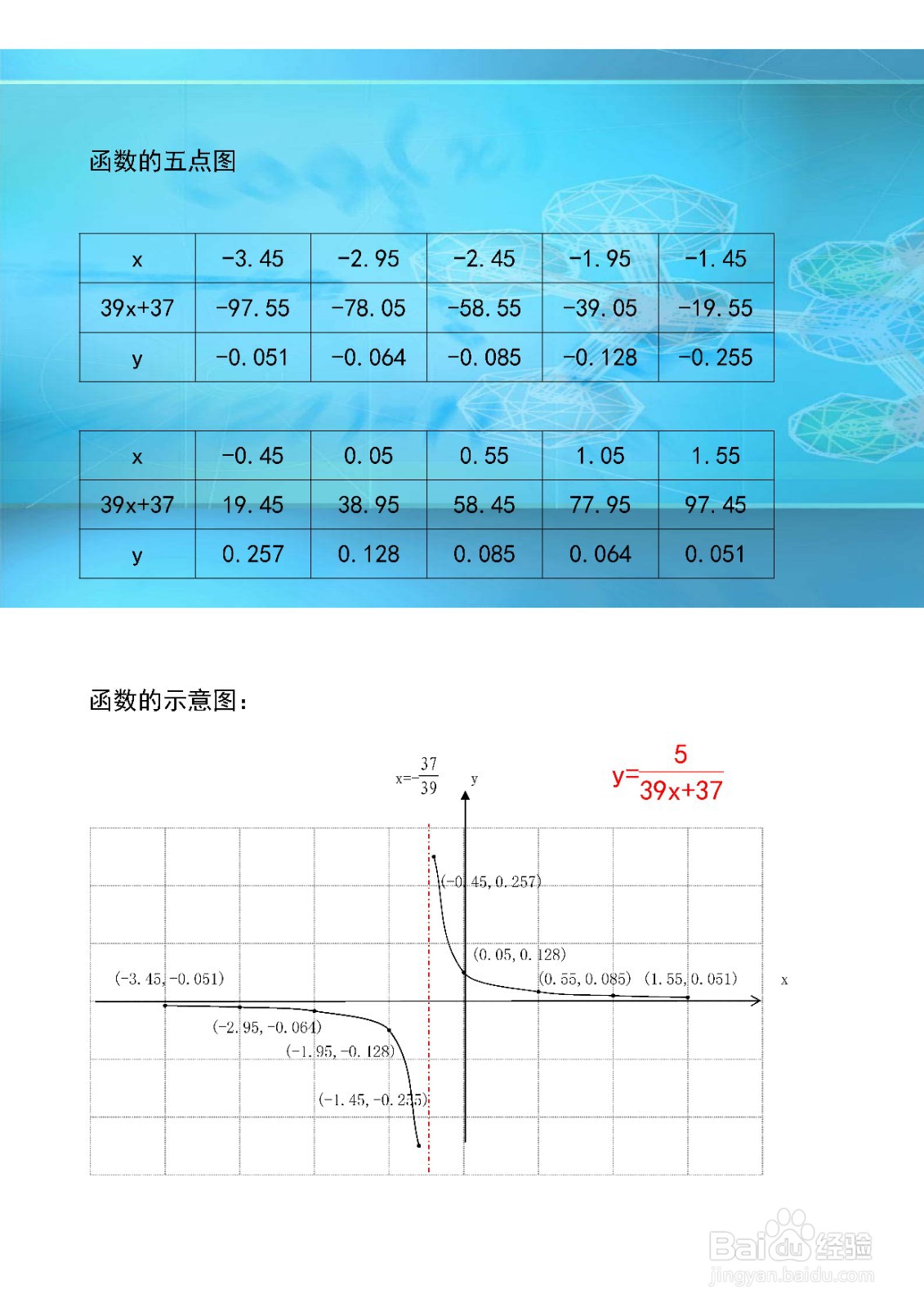
5、函数的示意图，综合以上函数的性质，函数y=5/(39x+37)的示意图如下：

6、 函数单调性是针对某一个区间而言的，是一个局部性质。因此，说单调性时最好指明区间。有些函数在整个定义域内是单调的;有些函数在定义域内的部分区间上是增函数，在部分区间上是减函数稆糨孝汶;有些函数是非单调函数，如常数函数。