怎么处理大量数据的拟合(线性规划处理)

在计算机的深度学习上面，我们要处理一大堆数据。但是，这需要一个前提，那就是数据拟合。我们要把离散的数据，拟合成一个可靠的函数。要找到合适的函数来逼近这些数据是不容易的，这又和线性规划扯上了关系。下面，我通过一个具体的例子，来介绍一下，怎么一步一步的拟合，又是怎么改进拟合结果的。

2、这个数据其实是二维的：因为数据是可数的，所以，我们可以把数据排列为第一个数字，第二个数字，等等。这样，就产生了一个函数关系，其自变量是正整数，而因变量是给定数据里面的数字，如f(1)=0.807243，f(2)=1.01259，……

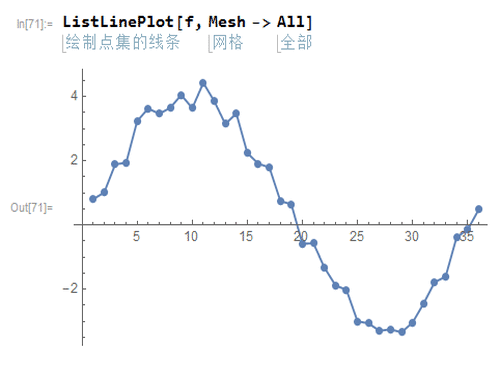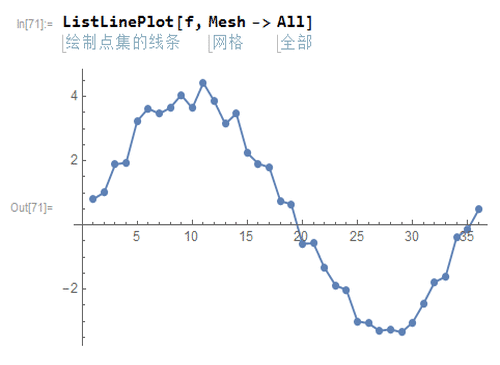
4、g如果构造出来了，有什么用呢？最简单的应用，就是预测近期数据。比如，给出前10000个数字，预测第10001个数字。一般的，离得越远，预测的可靠性越低，如天气预报。

2、我们考虑新数据与原数据之间的差方：(g(1)-f(1))^2，(g(2)-f(2))^2，……这些差方的平均值G，就体现新数据与原数据的差别，或者叫做拟合的误差。如果这个差别过大，那么这个g就不合适了。

4、检测是否是极小值：作G关于a的图像（注意，下图的图形不合比例），或者，直接证明，二次函数如果开口朝上，就有最小值。

一次函数

1、考虑一次函数。不过，我们需要关心的是，误差最小的拟合，所以直接找误差最小的一次函数。g[n_] := a*n + bh = g /@ Range[36];G = Table[((h[[n]]) - (f[[n]]))^2/36, {n, 1, 36}] // Total // Simplify;jie = Solve[{D[G, a] == 0, D[G, b] == 0}, {a, b}] // Flatten;Show[ListLinePlot[f, Mesh -> All],Plot[g[n] /. jie, {n, 0, 36}, PlotStyle -> Green]]拟合效果不好。

3、各个偏导数都等于0，才有可能找到使G取最小值的a和b。

5、其实，mathematica已经把这个拟合的过程，整合为一个内置命令了：h = a*n + b;FindFit[f, h, {a, b}, n]

2、再试试三次函数，G是关于a、b、c、d的四元函数。注意：此时的G的图像，已经不太可能绘制出来了。但我们仍旧可以证明，G存在最小值。这个的拟合效果，就很好啦。

试试其它函数的拟合

1、试试正弦函数与一次函数的复合函数：a*sin(b*n+c)+d

3、别的情形还有无线多，读者有兴趣的话，可以自己去尝试，这里就不再继续举例。