【微分几何】圆环面上测地线的周期性

1、圆环面方程式是：r = RotationTransform[v, {0, 0, 1}][{Cos[u] + 2, 0, Sin[u]}];如果a和b的螋菟钾兹曲纹坐标如下：{a, b} = {{0, 0}, {Pi/3, Pi/30}}那么经过a和b的测地线如下图所示。

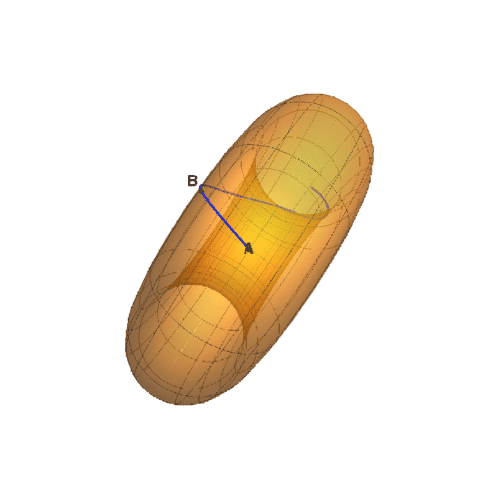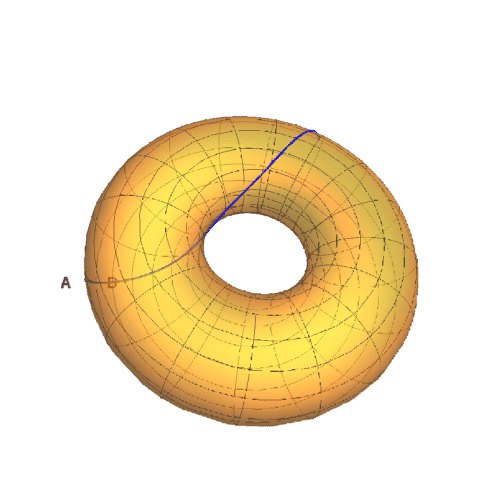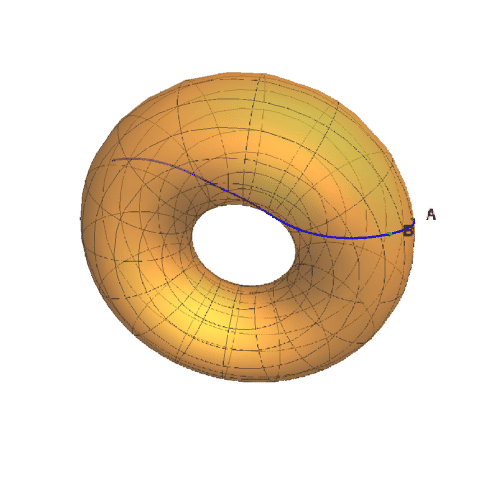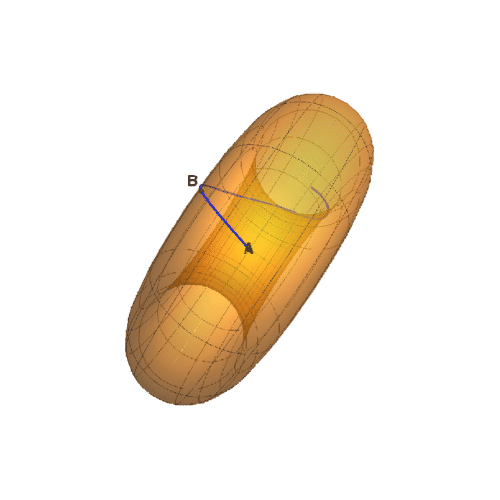
2、绘制这条测地线的弧长公式的图像，能够明显看到弧长周期性的递增。

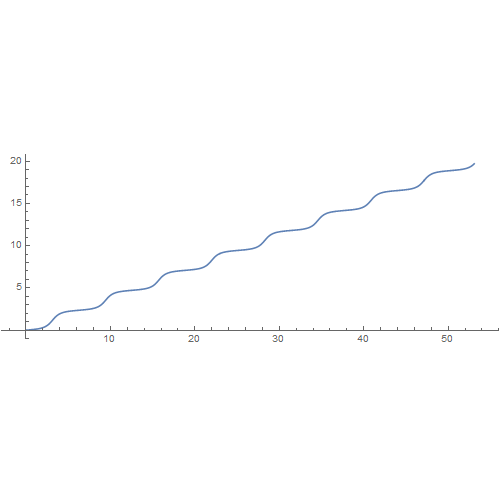
3、而继续延长这条测地线，也可以发现明显的【周期缠绕】。

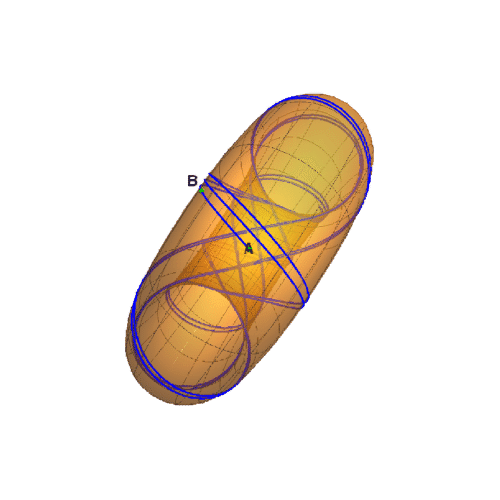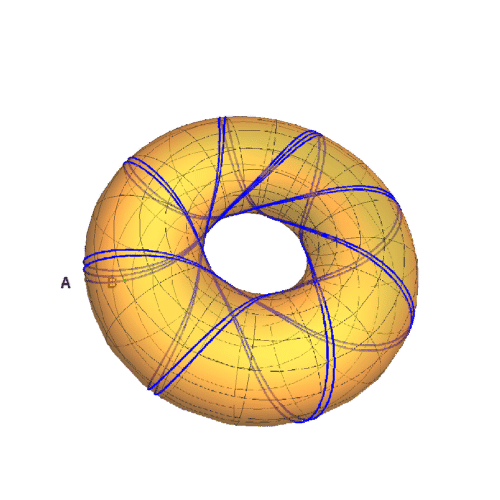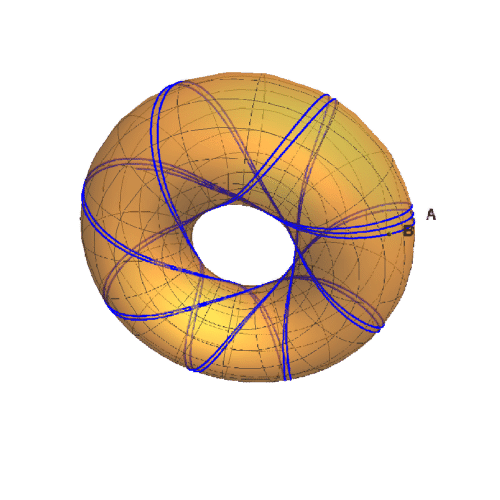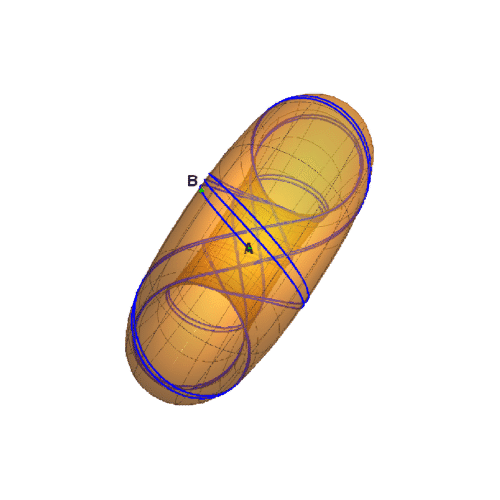
4、下面，来看一下这条测地线缠绕的动画效果：

5、更换a和b的曲纹坐标：{a, b} = {{0, 0}, {Pi/3, Pi/10}};此时的测地线，是不稳定的，缠绕的时候，不允许绷紧，否则会脱离圆环面。

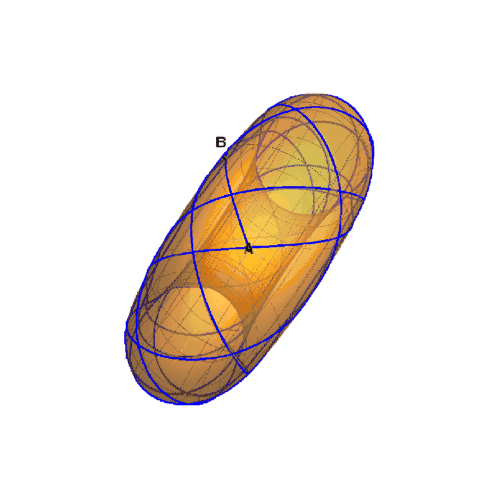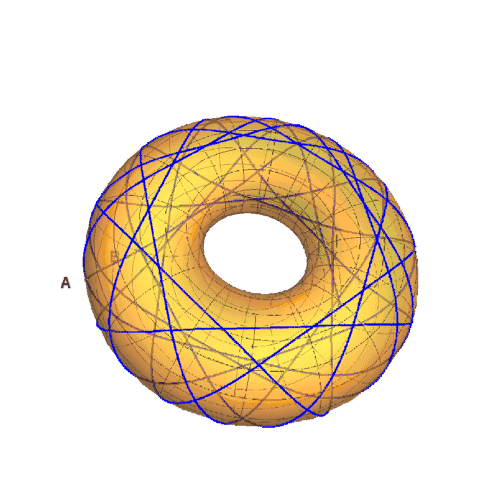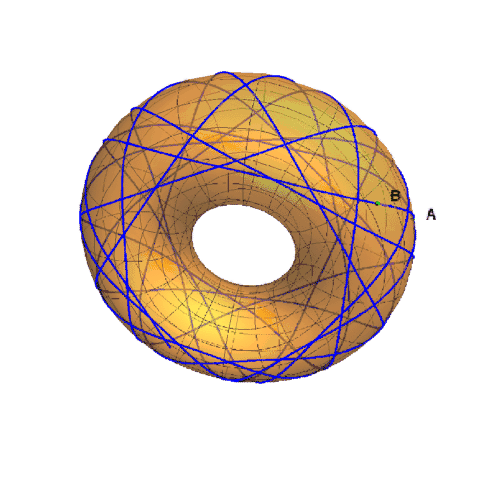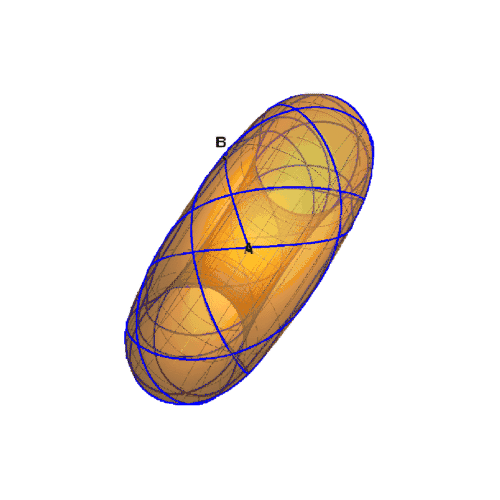
6、测地线的曲纹坐标的关系，满足如下图像。

7、相应的缠绕动画：

8、多缠绕几圈，得到如下图形：