三角函数y1=cosx/5与y2=sin2x/7的交点

1、本经验中，余弦函数y1=cosx/5和正弦函数y2=sin2x/7在同一直角坐标系的示意图如下所示，可见函数的交点在x轴上下交替出现。

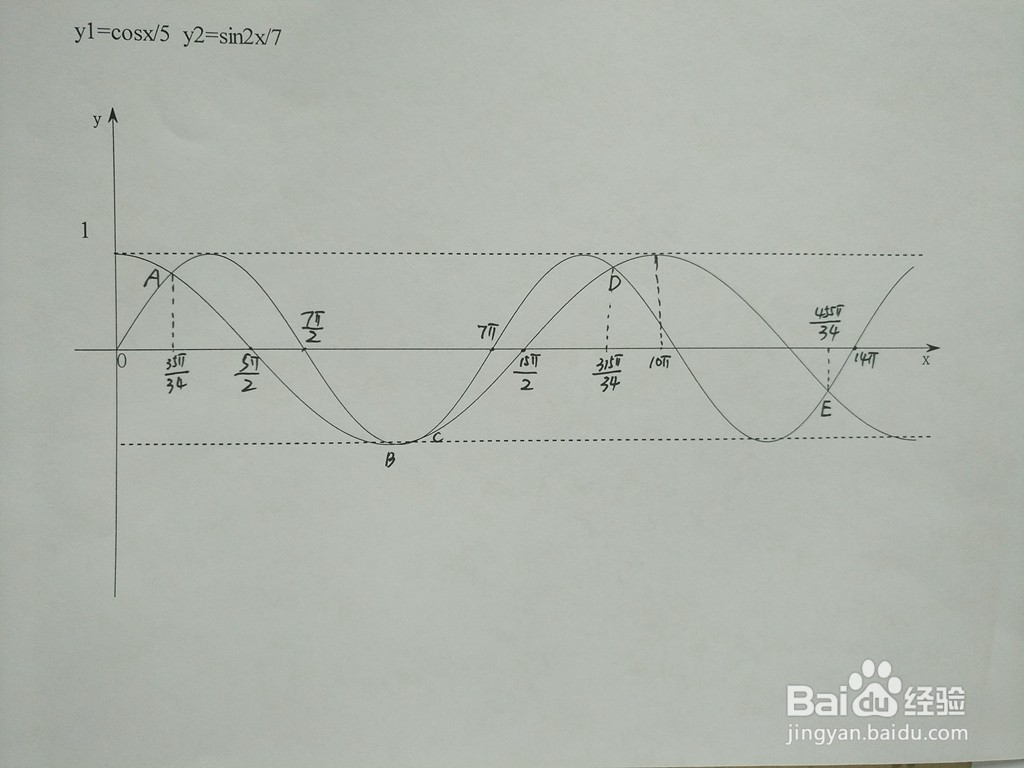
4、进一步解析两个三角函数y1=cosx/5与y2=sin2x/7交点横坐标通式。即x1=70/3kπ+35π/6,x2=70π/17+35π/14.

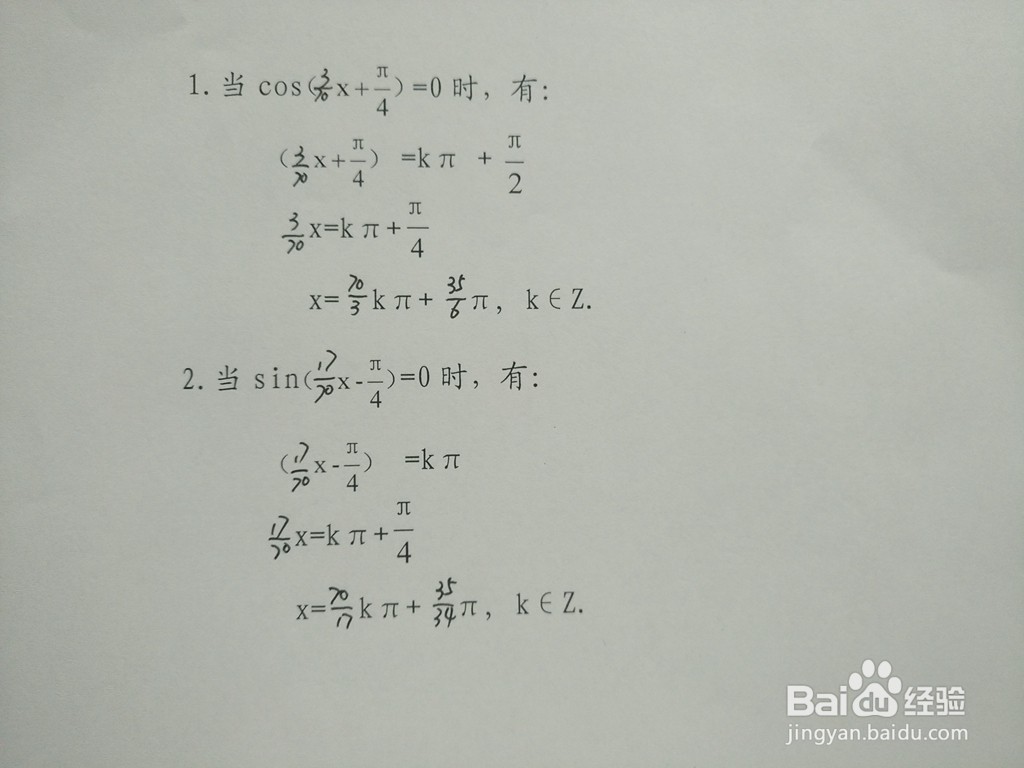
6、函数交点，两函数y1=cosx/5与y2=sin2x/7在部分周期内，交点坐标如下：如A（35π/34,cos7π/34）.

7、对于任意一个实数x都对应着唯一的角，而这个角又对应着唯一确定的正弦值sin x，这样，对于任意一个实数x都有唯一确定的值sinx与它对应，按照这个对应法则所建立的函数，表示为f(x)=sinx，叫作正弦函数。