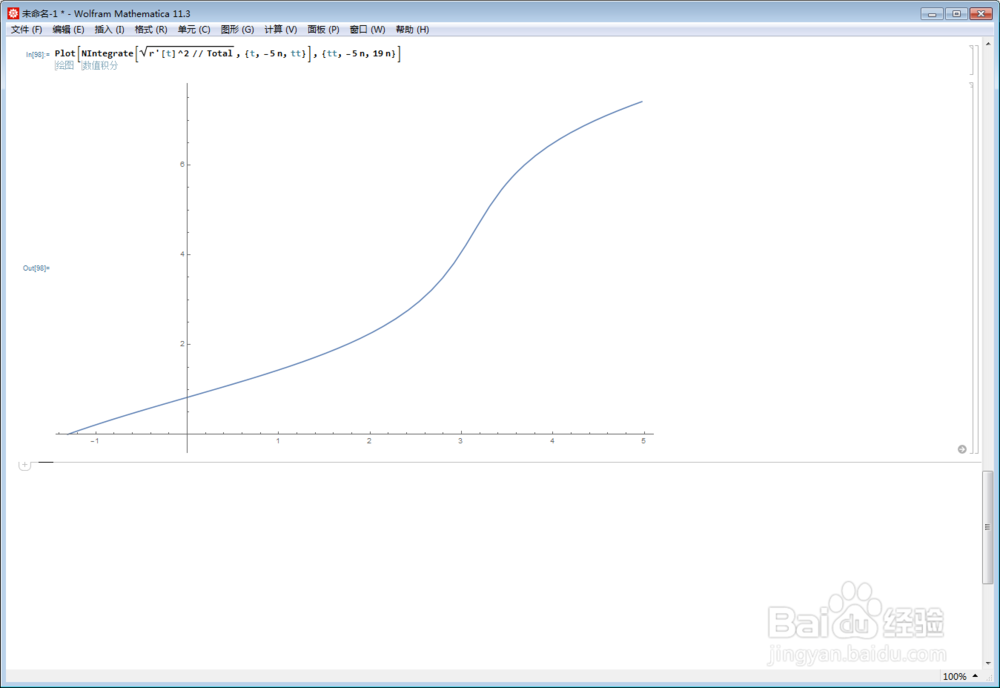
【微分几何】参数与弧长不对称的中心对称图形
1、先绘制参数方程的横坐标的图像:

2、观察图像,发现有四个极值,算之:

3、经过计算发现,这四个极值,是两个最小值和两个最大值,在参数方程的图像里面,表示为两个左顶点和两个右顶点。
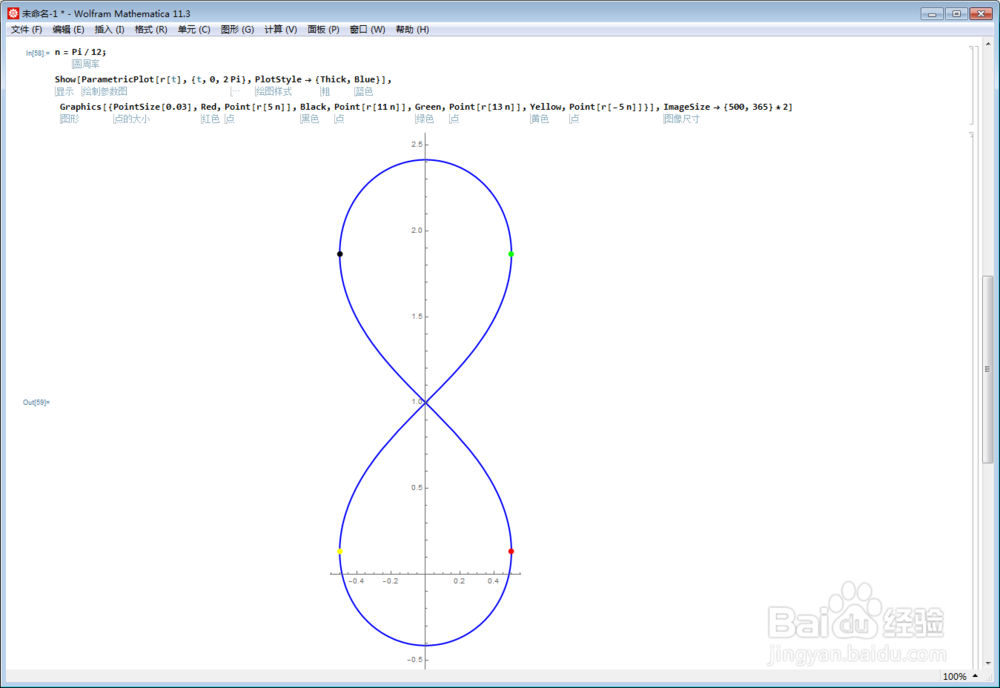
4、计算弧长,按照上图的黄、红、绿、黑四点的顺序进行;直接用Mathematica作弧长图像:
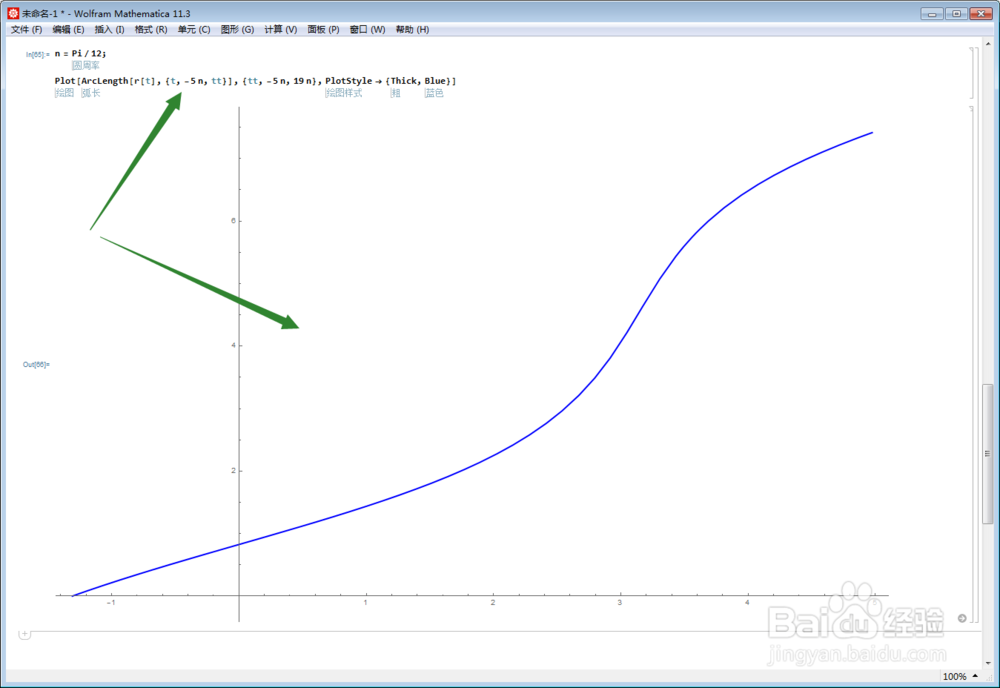
5、根据胡长公式来计算弧长:
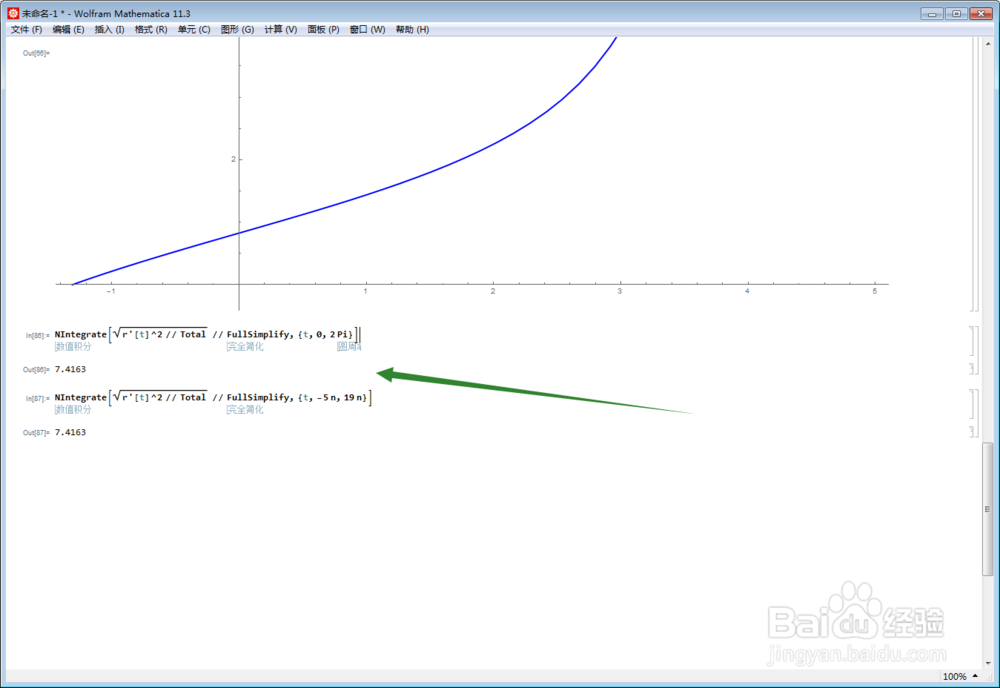
6、看看,能不能用不定积分,来表示弧长函数。结果显示,原函数不是初等函数。
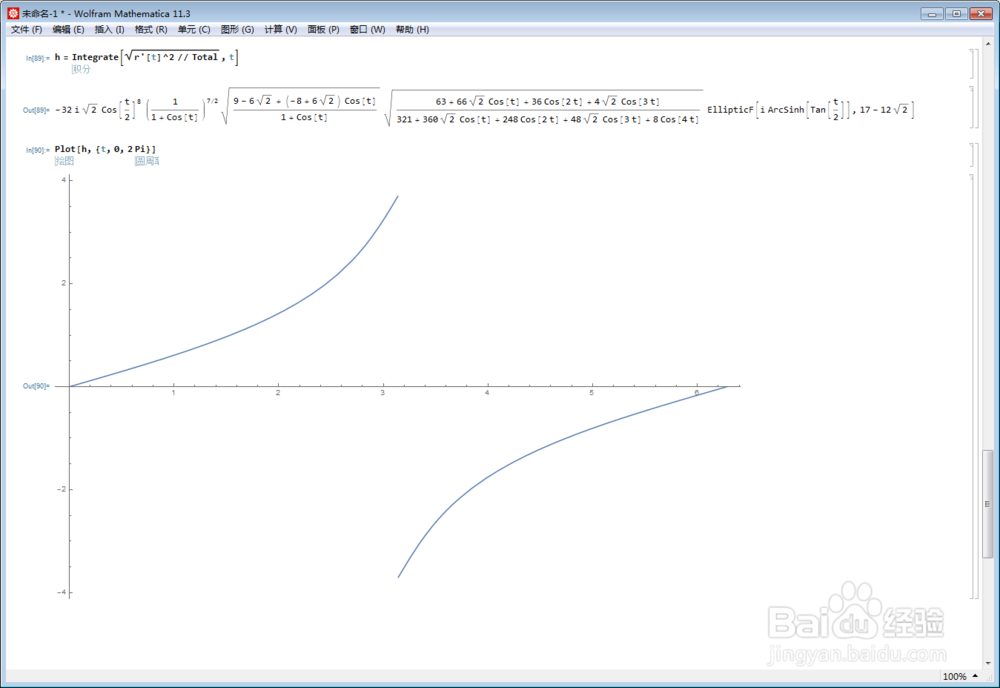
7、弧长公式是难以计算的,退而求其次,采用数值积分来塥骈橄摆计算弧长。这与步骤4的结果是一致的。明显看出,弧长的增长速率,是先缓后急。也正是因此,才导致【中心对称】的性质,难以验证。