Mathematica解几何题一则

1、设C为原点，B为{-a,0}，AB=b，AC=c，那么就有约束条件 a>0&&b>0&&c>0&&b>c。这里的计算量是巨大的，如果是手工算，无意是在翻山越岭。

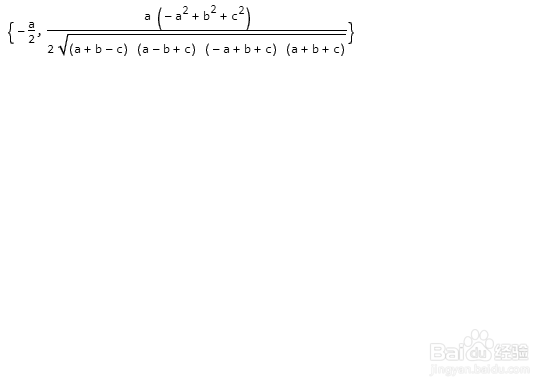
3、F的坐标可以表示为：{((Abs[((Abs[a])^((-1))*((b)^(2)+((c)^(2像粜杵泳)*(-1)))*1/2)])^((-1))*(Abs[a])^((-1))*(((c)^(2)*(b)^(2)*(a)^(2))+((c)^(2)*(b)^(4))+((c)^(4)*(a)^(2)*(-1))+((c)^(4)*(b)^(2)*(-2))+(c)^(6)+(Abs[((Abs[a])^((-1))*((b)^(2)+((c)^(2)*(-1)))*1/2)]*((Abs[a]*(b)^(2)*(a)^(2)*(-2))+(Abs[a]*(b)^(4)*2)+(Abs[a]*(c)^(2)*(a)^(2)*4)+(Abs[a]*(c)^(2)*(b)^(2)*(-2)))))*(((b)^(2)+((c)^(2)*(-1))))^((-1))*(a)^((-1))*1/4),((Abs[((Abs[a])^((-1))*((b)^(2)+((c)^(2)*(-1)))*1/2)])^((-1))*(Abs[a])^((-1))*(((c)^(2)*(b)^(2))+((c)^(4)*(-1))+(Abs[((Abs[a])^((-1))*((b)^(2)+((c)^(2)*(-1)))*1/2)]*Abs[a]*(b)^(2)*2))*(((b)^(2)+((c)^(2)*(-1))))^((-1))*(((b*(-1))+c+Abs[a]))^((-1/2))*((b+(c*(-1))+Abs[a]))^((-1/2))*((b+c+(Abs[a]*(-1))))^((-1/2))*((b+c+Abs[a]))^((-1/2))*((a)^(4)+((b)^(2)*(a)^(2)*(-2))+(b)^(4)+(c)^(4)+((((a)^(2)*(-2))+((b)^(2)*(-2)))*(c)^(2)))*(a)^((-1))*(-1/4))}

5、用向量法计算∠ODF的角度：((Pi*1/2)+(ArcTan[(((((b)^(2)*(a)^(2)像粜杵泳)+((b)^(4)*(-1))+((c)^(2)*(a)^(2)*(-1))+((c)^(2)*(b)^(2)*(-2))+((c)^(4)*3)+(Abs[((Abs[a])^((-1))*((b)^(2)+((c)^(2)*(-1)))*1/2)]*((Abs[a]*(a)^(2)*2)+(Abs[a]*(b)^(2)*(-6))+(Abs[a]*(c)^(2)*(-2))))))^((-1))*(((b)^(2)*(-1))+(c)^(2)+(Abs[((Abs[a])^((-1))*((b)^(2)+((c)^(2)*(-1)))*1/2)]*Abs[a]*2))*(((b*(-1))+c+Abs[a]))^((-1/2))*((b+(c*(-1))+Abs[a]))^((-1/2))*((b+c+(Abs[a]*(-1))))^((-1/2))*((b+c+Abs[a]))^((-1/2))*((a)^(4)+((b)^(2)*(a)^(2)*(-2))+(b)^(4)+(c)^(4)+((((a)^(2)*(-2))+((b)^(2)*(-2)))*(c)^(2))))]*(-1)))