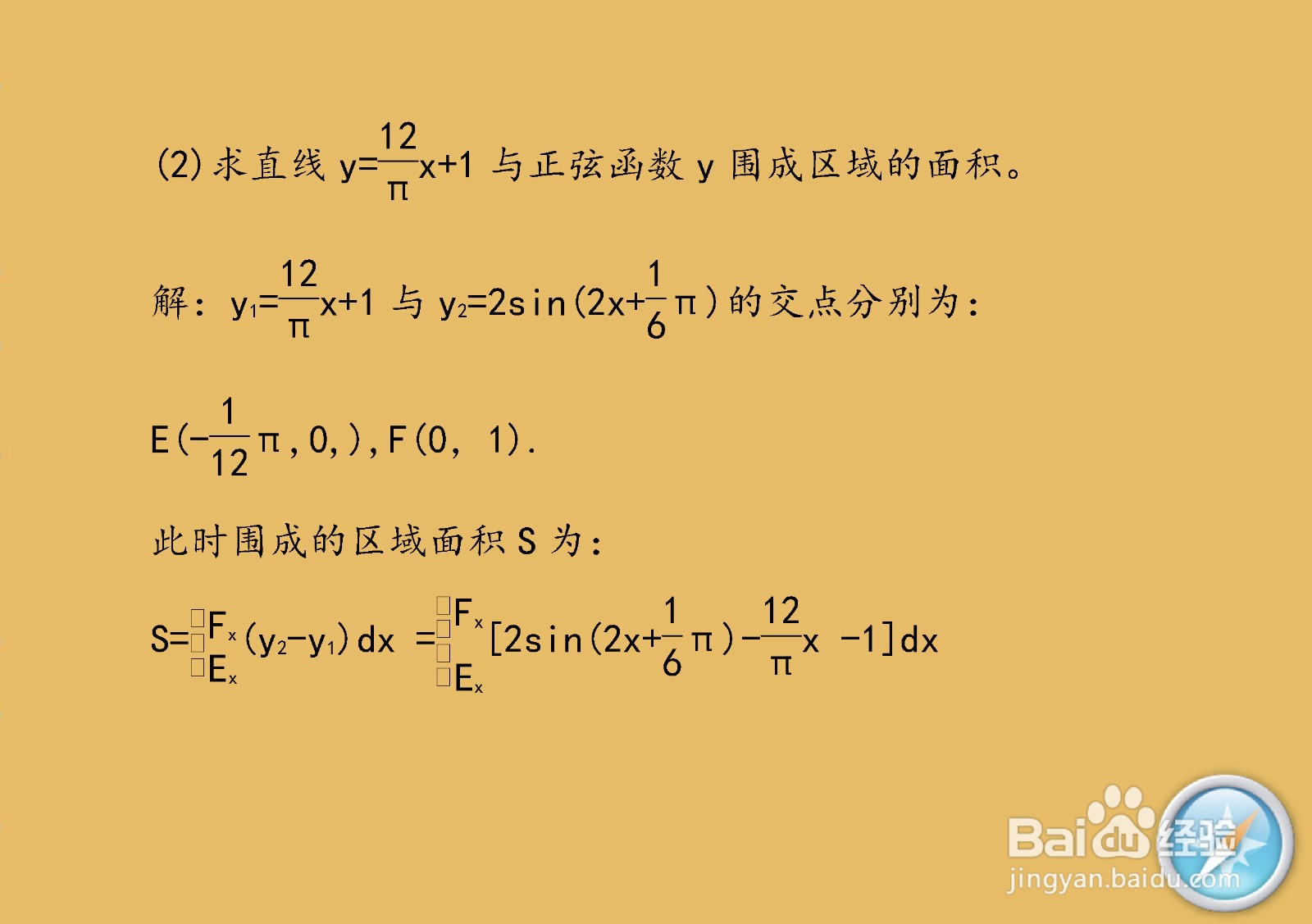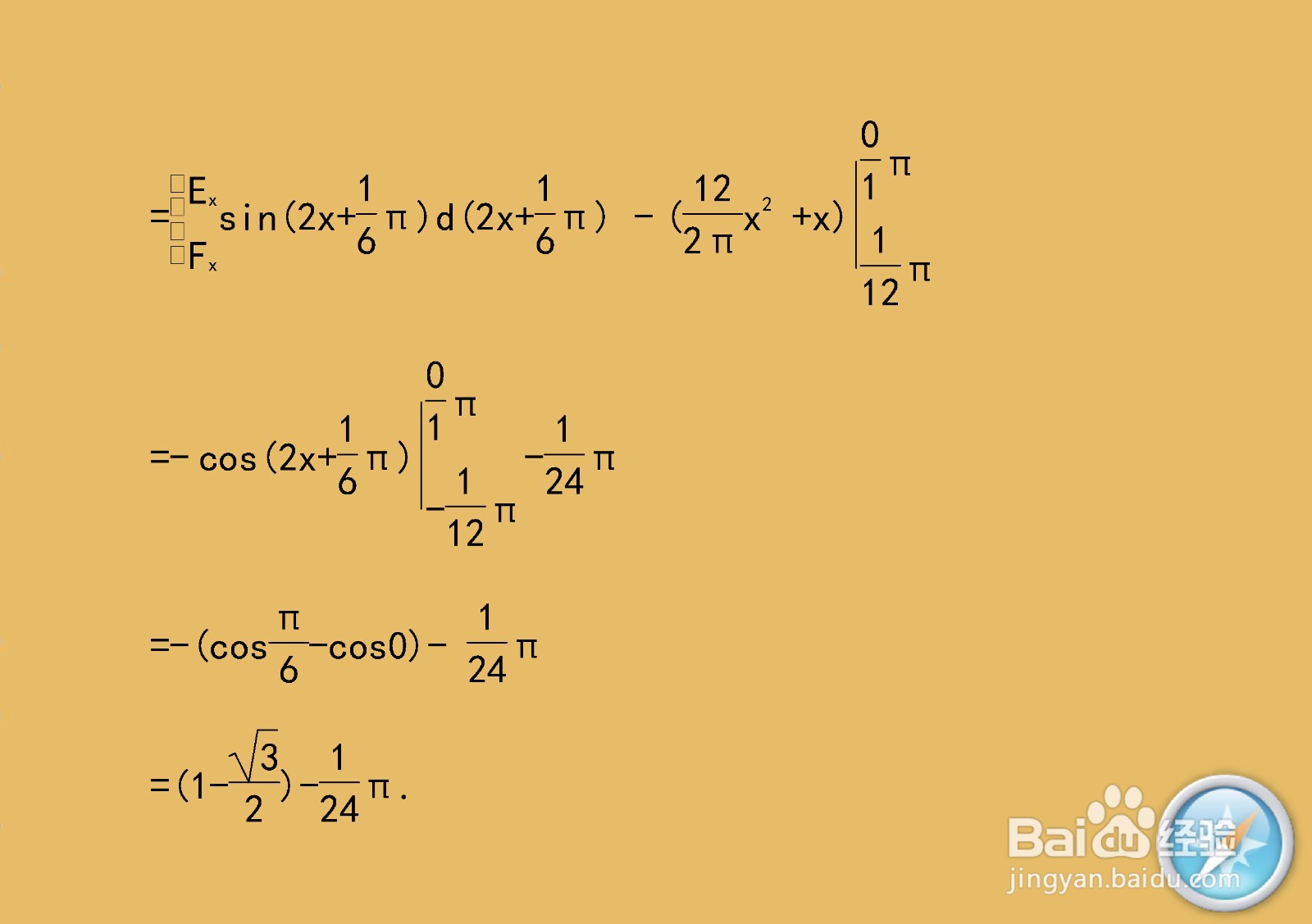解析正弦三角函数y=2sin(2x+π/6)的性质

主要内容,本文主要归纳三角函数y=2sin(2x+π/6)的定义域、值域、单调、周期、对称轴、切线等有关性质。

工具/原料

正弦函数性质

定积分与区域面积

导数与函数性质

三角函数性质归纳

1、 三角正弦函数的定义域、值域和最小正周期等基本性质如下。 定义域：正弦三角函数的定义域为全体实数，即定义域为（-∞，+∞）。 值域：正弦函数y=sinx的值域为[-1,1],则本题y=2sin(2x+16π)的值域为：[-2,2]. 最小正周期：函数的最小正周期为:T=2π/2=π。

2、正弦三角函数的对称轴和对称中心的求解。当2x+1/6π=0时，有：x=-1/12π.即该函数y的中心对称点为：（-1/12π，0）。

3、由正弦函数的导数公式y=sinx，y'=cosx,即可求解该正弦函数的一阶导数、二阶导数，并和推解其高阶导数。

4、根据基本正弦函数y=sinx的单调增区间，即可推导求出正弦复合函数的单调增区间。(1拘七呷憎)单调增区间2kπ-π/2≤2x+1/6π≤2kπ+π/2,k∈Z，2kπ-π/2-1/6π≤2旌忭檀挢x≤2kπ+π/2-1/6π,2kπ-2/3π≤2x≤2kπ+1/3π，kπ-1/12π≤x≤kπ+1/6π即该函数的单调增区间为:[kπ-1/12π, kπ+1/6π]

5、根据基本正弦函数y=sinx的单调减区间，即可推导求出正弦复合函数的单调减区间。2k息遴颞阈π+π/2≤2x+1/6π≤2kπ+3π/2,k∈Z，2kπ+π/2-1/6π攒炎欧艘≤2x≤2kπ+3π2+1/6π,2kπ+ 1/3π≤2x≤2kπ+5/3π，kπ+1/6π≤x≤kπ+5/6π即该函数的单调增区间为:[kπ+1/6π, kπ+5/6π]

6、 用导数知识，求解函数在点A(0,1)和B(13π/12,-√2拘七呷憎)处切线的主要过程和步骤。(1)函数的一阶导数：解：y=2sin(2x+1/6π)，则：y'=4cos(2旌忭檀挢x+1/6π)=2*2sin[2(x+π/2*1)+1/6π],(2)函数的二阶导数：y''=-4*2sin(2x+1/6π)=-2*22sin[2(x+π/2*2)+1/6π],(3)函数的高阶导数。y(n)=(-1)n-1/2*2nsin[2(x+π/2*n)+1/6π],n≥1.

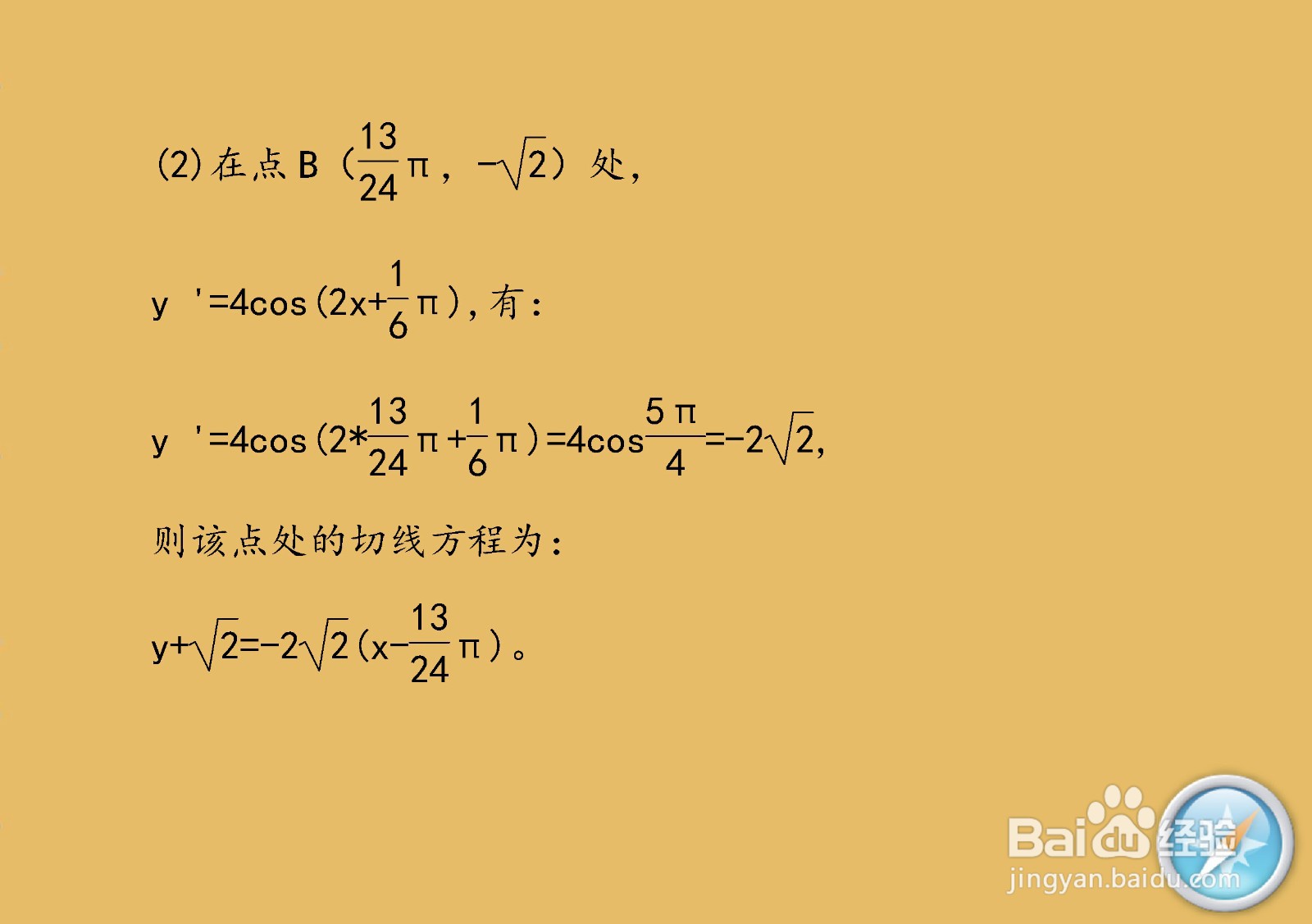
7、按照定积分与曲顶围成区域的面积关系，计算该正弦函数在半个周期的与坐标轴围成的区域的面积，主要步骤为：解：先求其中半个周期内x的坐标点，即：C(-1/12π,0),D(1/6π,0).

8、举例介绍计算直线与正弦函数围成的区域面积的主要方法与步骤。