函数y=√(37x+9)+√(12x+41)的性质及其图像解析

1、函数是一种映射关系，它将一个集合（定义域）中的每一个元素按照一定的法则（对应关系）与另一个集合（值域）中的元素一一对应。在这个映射过程中，定义域起着至关重要的作用。它不仅决定了函数的存在性，而且还影响着函数y=√(37x+9)+√(12x+41)的性质和应用。

2、如果函数y=f(x)在区间D内可导(可微)，若x∈D时恒有f'(x)>0，则函数y=f(x)在区间D内单调增加;反之，若x∈D时，f'(x)<0,则称函数y=f(x)在区间D内单调减少。

3、如果一个函数f(x)在某个区间I上有f''(x)(即二阶导数)>0恒成立，那么在区间I上f(x)的图像上的任意两点连出的一条线段，这两点之间的函数y=√(37x+9)+√(12x+41)图像都在该线段的下方，反之在该线段的上方。

4、函数y=√(37x+9)+√(12x+41)图像五点示意图，列图表解析函数y=√(37x+9)+√(12x+41)上的五点图如下表所示。

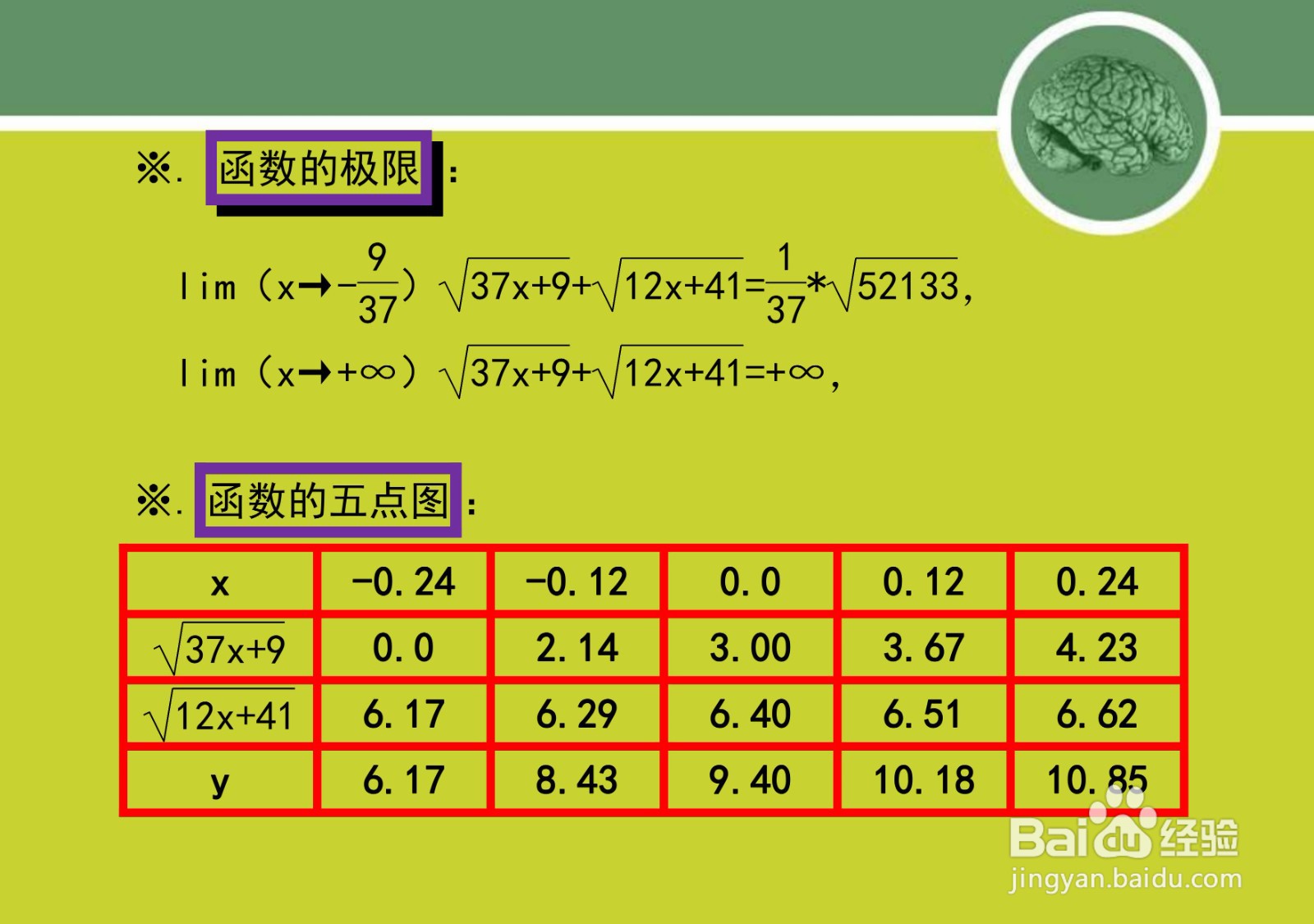
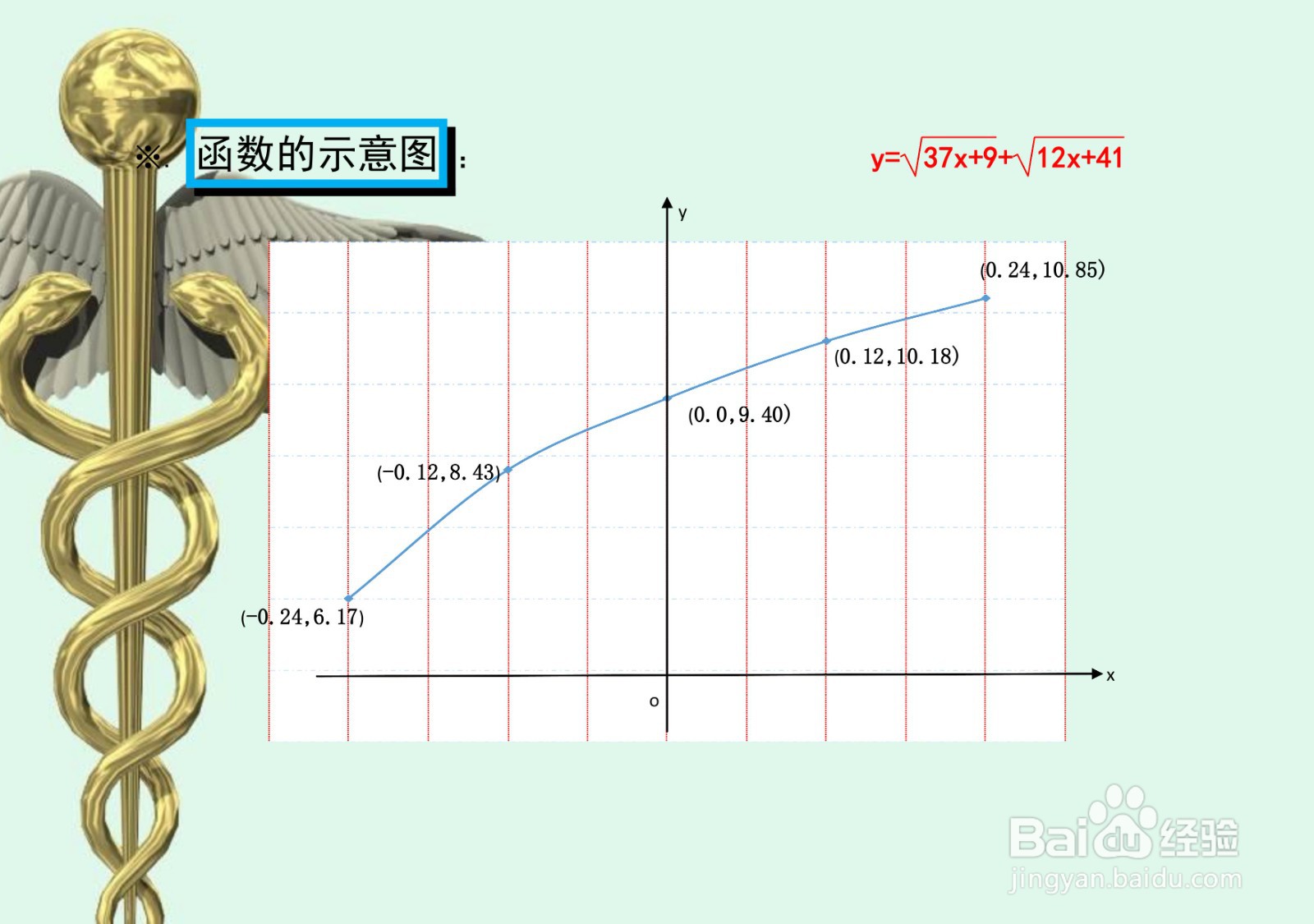
5、根据以上函数y=√(37x+9)+√(12x+41)的定义域，以及函数的单调性、凸凹性等，即可简要画出函数y=√(37x+9)+√(12x+41)的示意图如下：