导数画复合对数函数y等于ln(-x.8)的图像示意图

1、 函数为自然对数函数的复合函数，根据函数特征，自变量可以取负数，即定义域为：(-∞，0）。

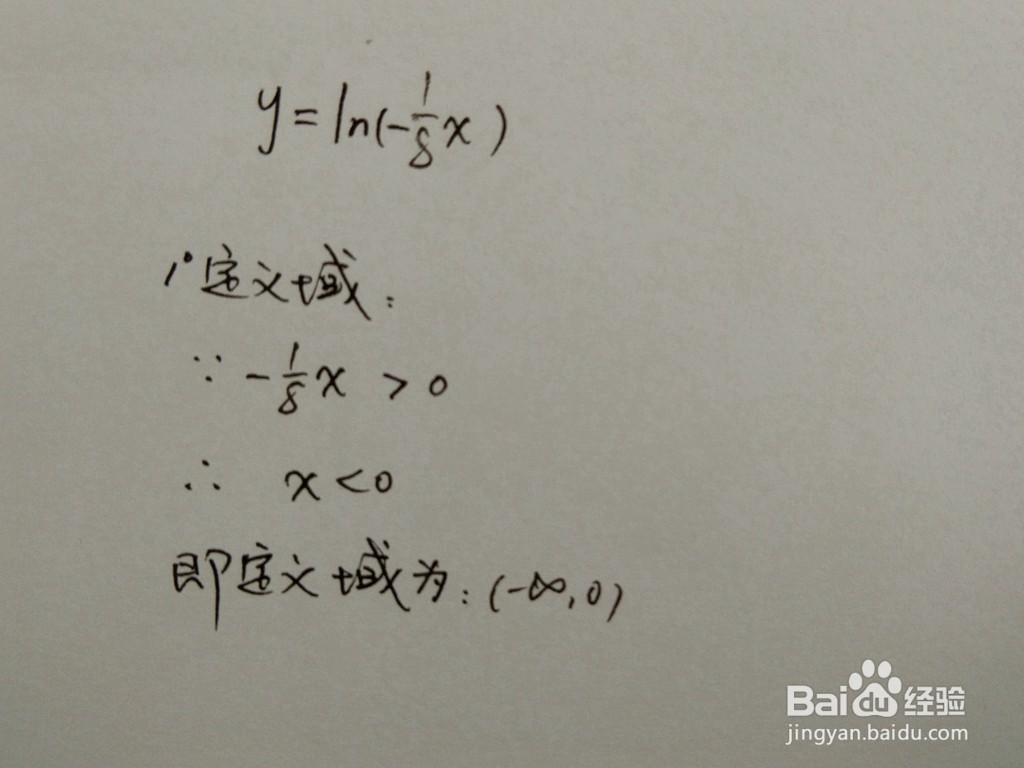
2、 函数的单调性，求出函数的一阶导数，通过函数的一阶导数的符号，判断函数的单调性。 函数的单调性也叫函数的增减性。当函数 f(x) 的自变量在其定义区间内增大(或减小)时，函数值f(x)也随着增大(或减小)，则称该函数为在该区间上具有单调性。

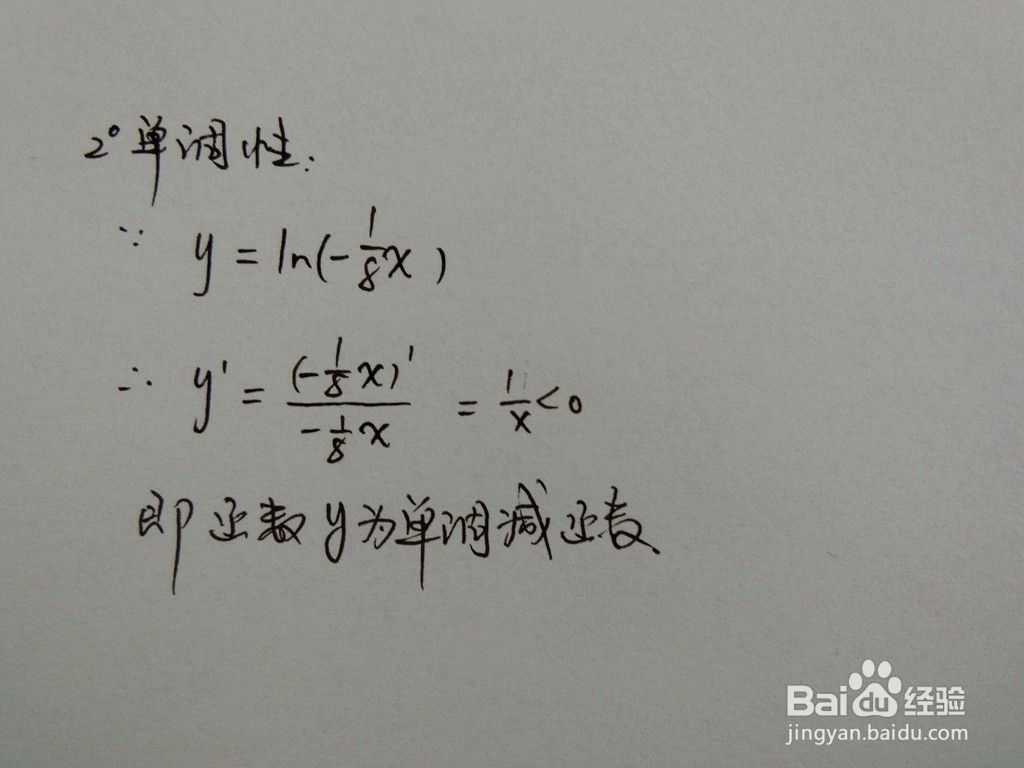
3、 函数的凸凹性，通过函数的二阶导数，解析函数的凸凹性。 二阶导数，是原函数导数的导数，将原函数进行二次求导。一般的，函数y=f(x)的导数y'=f'(x)仍然是x的函数，则y'=f'(x)的导数叫做函数y=f(x)的二阶导数。

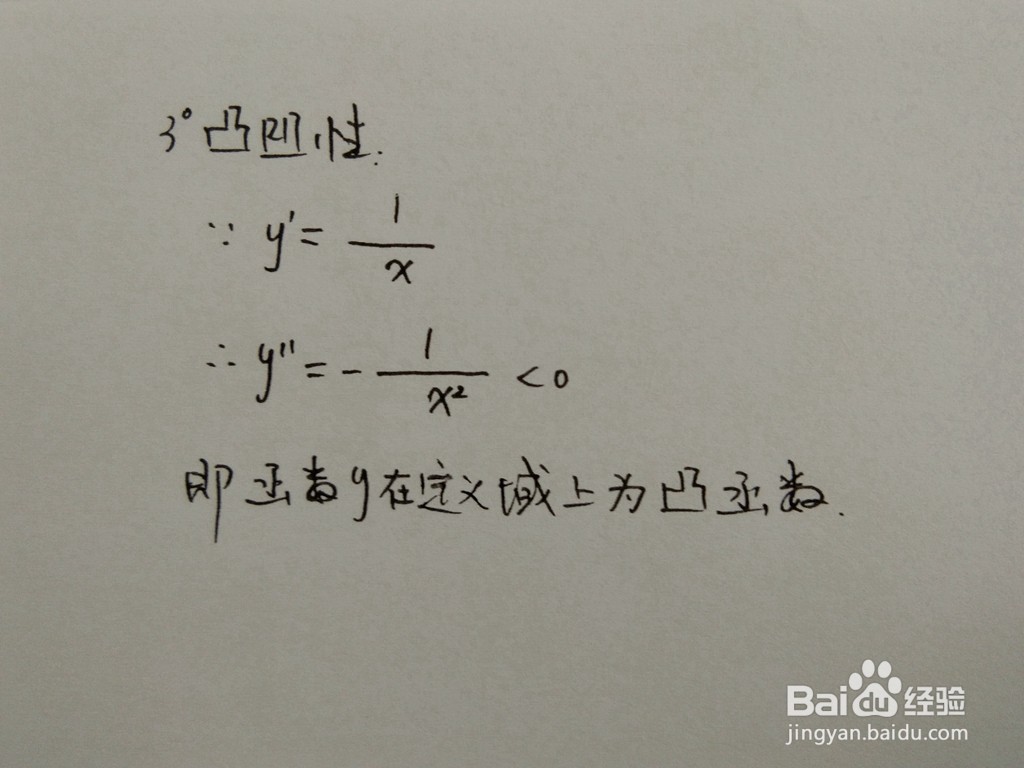
4、 设函数f(x)在x0处的某一去心邻域内有定义，若存在常数A，对于任意ε>0，总存在正数δ，使得当|x-xo|<δ时，|f(x)-A|<ε成立，那么称A是函数f(x)在x0处的极限。 函数的极限，函数在端点处的极限。

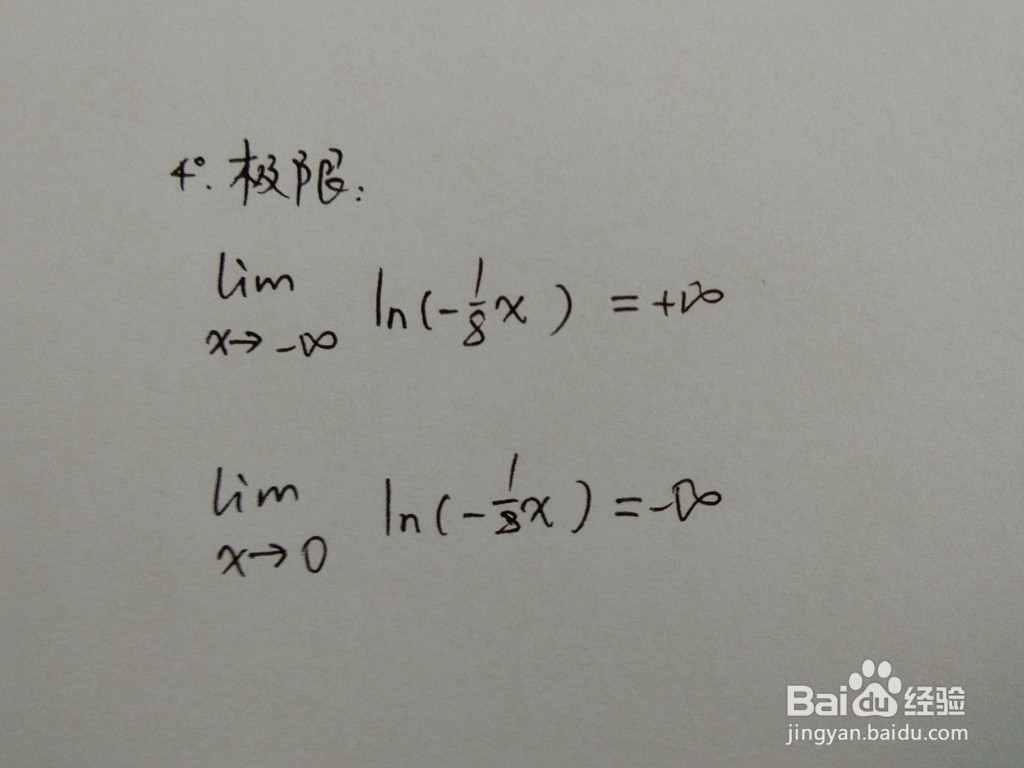
5、函数的五点图表如下图所示。

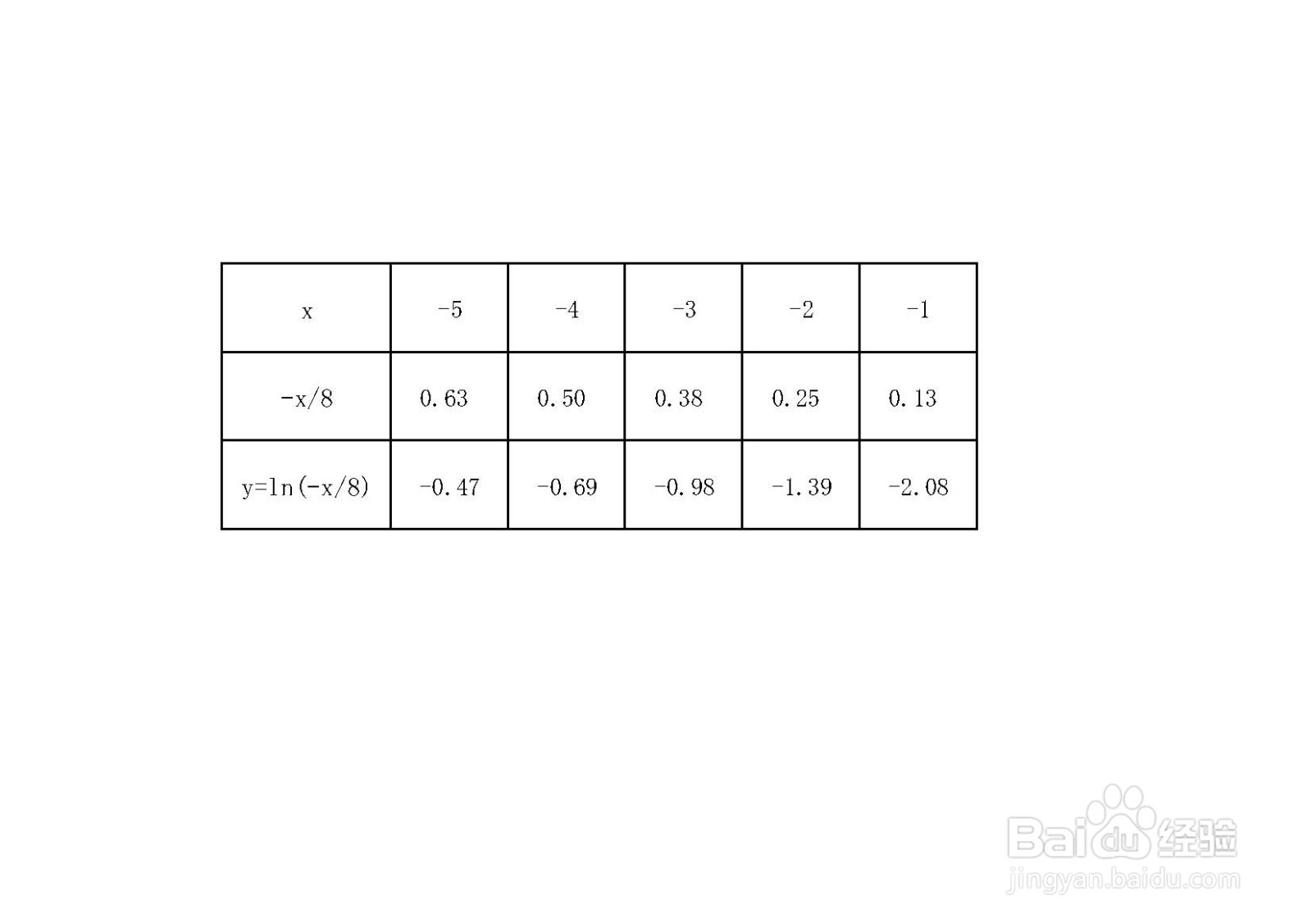
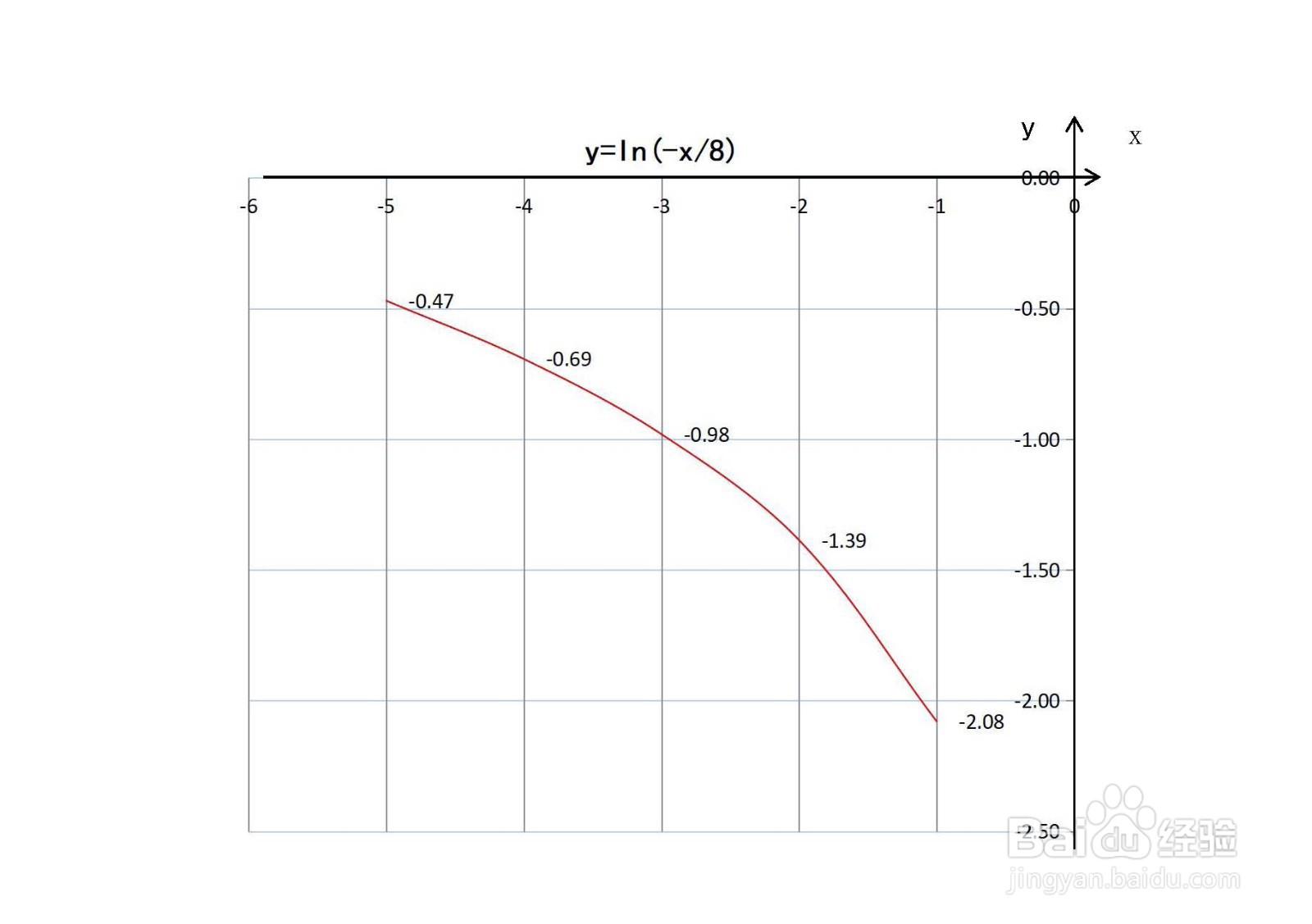
6、函数的示意图，综合以上函数的性质，函数的示意图如下：