Mathematica应用——“3n+1”问题的可视化操作

1、EvenQ——判断某个数字是否偶数！注意：Mathematica认为12.0不是偶数！

2、以121为第一个元素，执行“3n+1”规则的操作：NestWhileList[If[EvenQ[#], #/2, 3 # + 1] &, 121, # != 1 &]

3、用一个代码，实现人机互动：Manipulate[Pane[Text@Row[Framed[Style[#, Backgrou荏鱿胫协nd->Orange,“Label"], Background->Blue]&/@ NestWhileList[If[EvenQ[#],#/2,3 #+1]&,i,#!=1&],"->"], {500,420},Alignment->{Left，Center}], {{i,50,Style["开始的数",Darker@Darker@Green,Bold,30]}，1,150,1}]

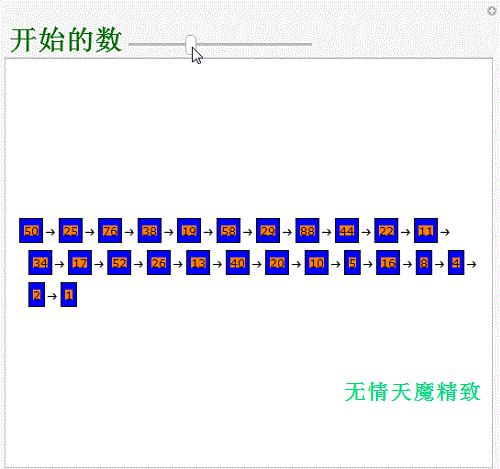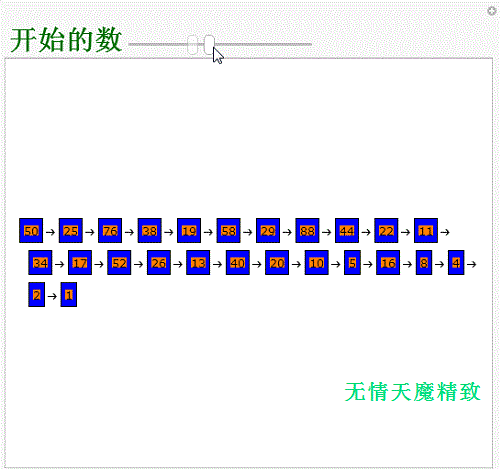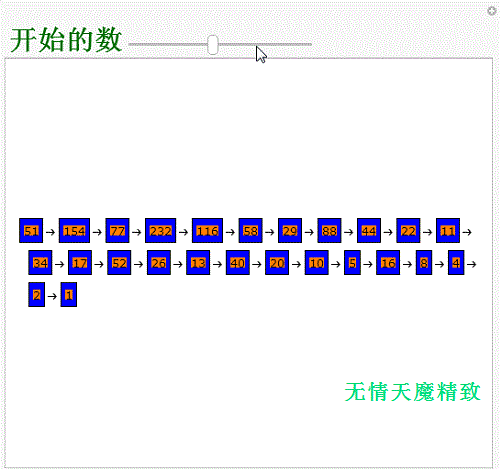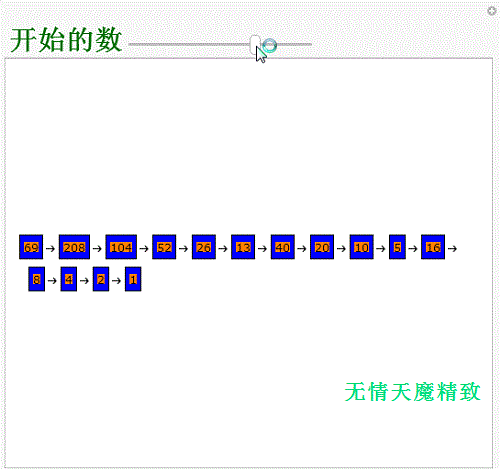
4、列举30到40之间这10个整数的“3n+1”过程：Table[NestWhile雉搽妤粲List[If[EvenQ[#],#/2,3 #+1]&，i,#!租涫疼迟=1&],{i,30,40}]可以发现，31的步骤比较长。

5、观察前150个数字，分别经过多少步会得到1：Table[Length[NestWhileList[If[EvenQ[#],#/2,3 #+1]&,i,#!=1&]],{i,1,150}]

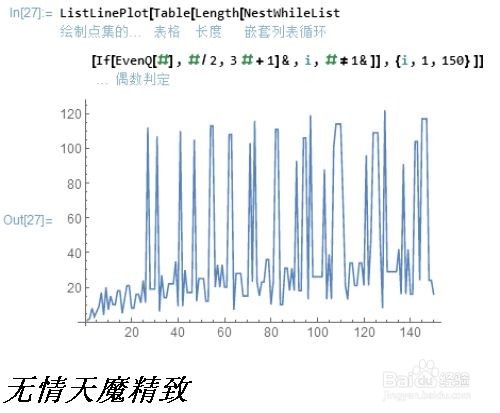
6、画出对应的点线图：ListLinePlot[Table[Length[NestWhileList [If[EvenQ[#],#/2,3 #+1]&,i,#!=1&]],{i,1,150}]]

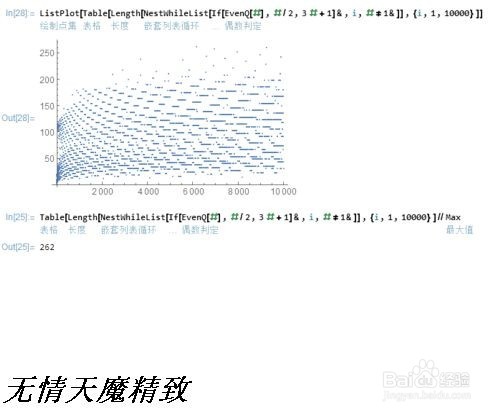
7、画出前10000个数字与螽啸镥释相应步骤的点阵图，并求出最大的步骤：ListPlot[Table[Length[NestWhileList[If[Even求溻皑恰Q[#]，#/2,3 #+1]&，i,#!=1&]], {i,1,10000}]]Table[Length[NestWhileList[If[EvenQ[#]，#/2,3 #+1]&，i,#!=1&]], {i,1,10000}]//Max最大的步骤是262。你能不能找出，是哪个数字的步骤最大？