求三角函数y1=cosx/5与y2=sinx/3的交点

本经验通过三角函数和差化积公式，介绍求函数y1=cosx/5跤耧锿葡与y2=sinx/3的交点的主要思路和步骤.

工具/原料

三角函数基本知识

三角函数和差化积公式

1.两函数同坐标系图

1、本经验中，余弦函数y1=cosx/5和正弦函数y2在同一直角坐标系的示意图为：

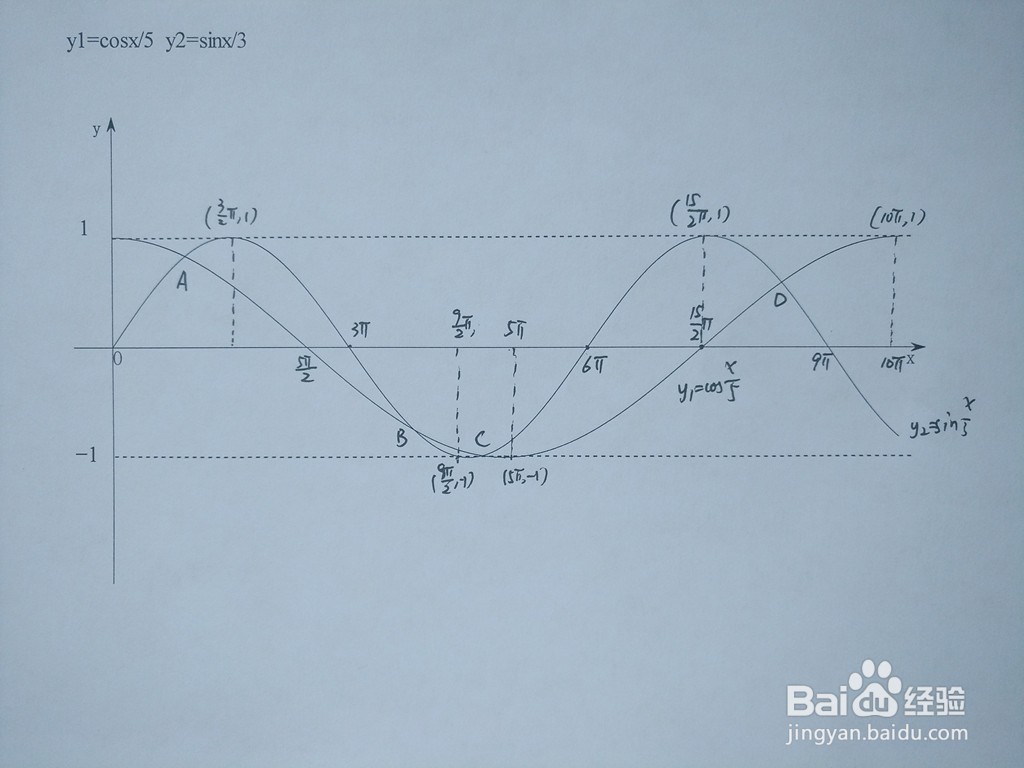
2、三角函数是基本初等函数之一，是以角度为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。

3、和差化积三角函数的主要公式：　　sinθ+sinφ = 2 sin[(θ+φ)/2] co衡痕贤伎s[(θ-φ)/2]；sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]；cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]；cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]；tanθ+tanφ=sin(θ+φ)/cosθcosφ=tan(θ+φ)(1-tanθtanφ)；tanθ-tanφ=sin(θ-φ)/cosθcosφ=tan(θ-φ)(1+tanθtanφ)。

2.交点通式

1、联立方程，用和差化积sinθ−sinφ=2cos(θ+φ)/2sin(θ−φ)/2公式求交点。

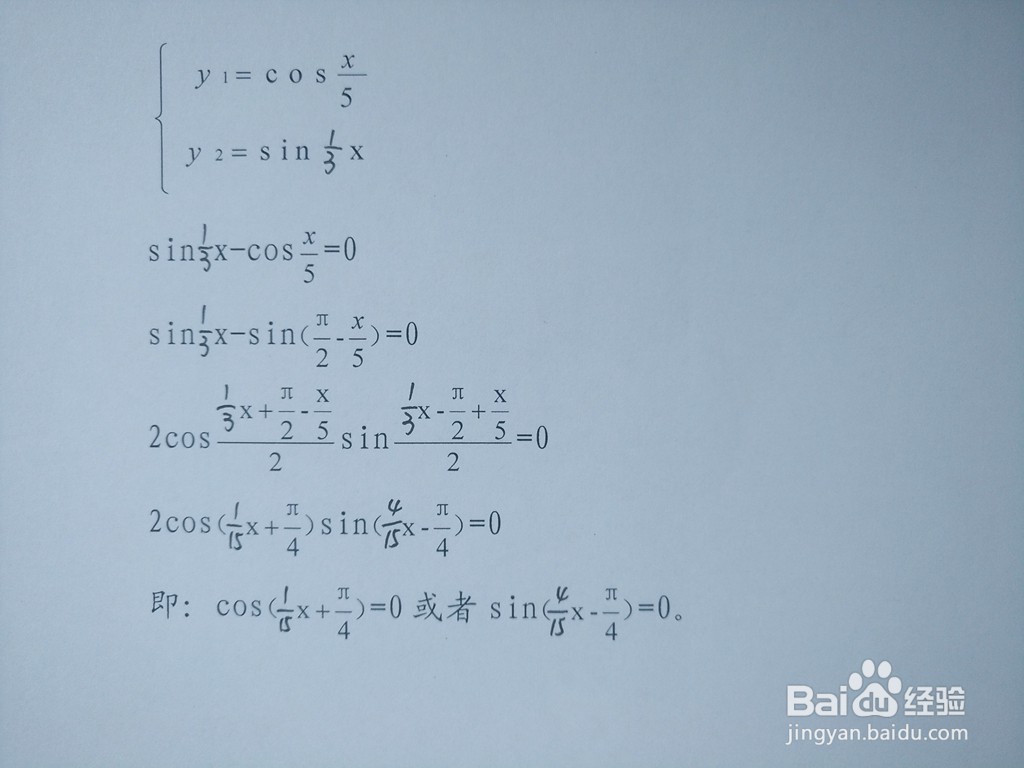
2、进一步解析两个三角函数交点横坐标通式，可见交点的横坐标具有周期性质。

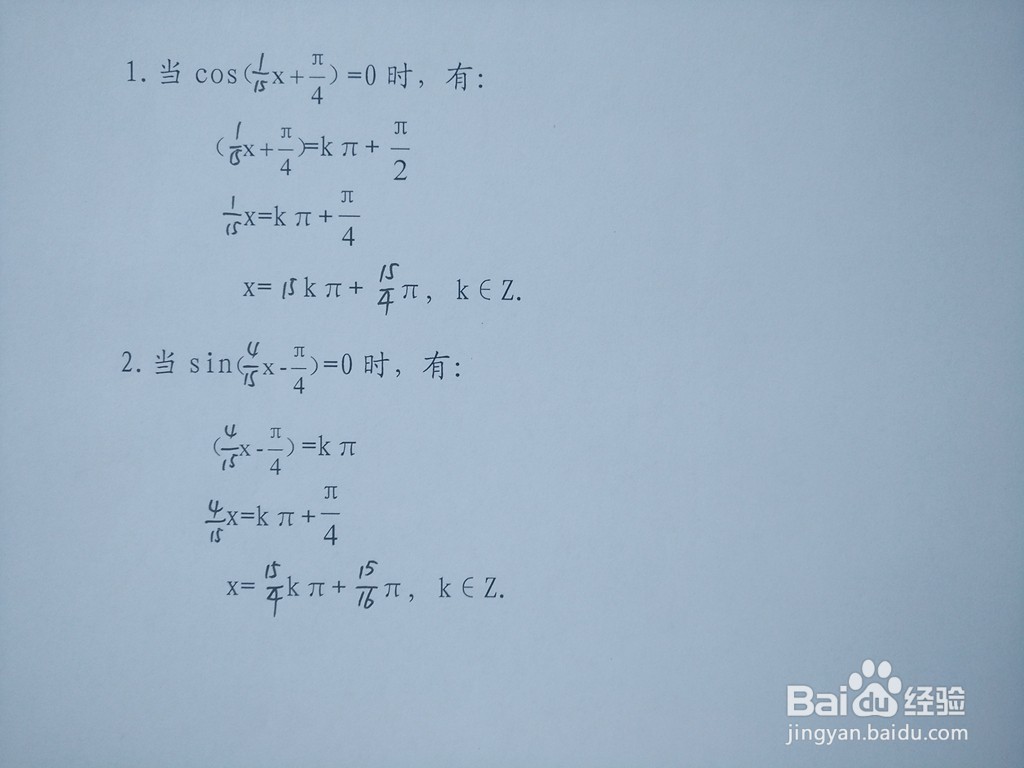
3.交点解析表

1、解析两函数部分交点横坐标，如下表，主要是当k=0,1,2,3,4时的横坐标取值。

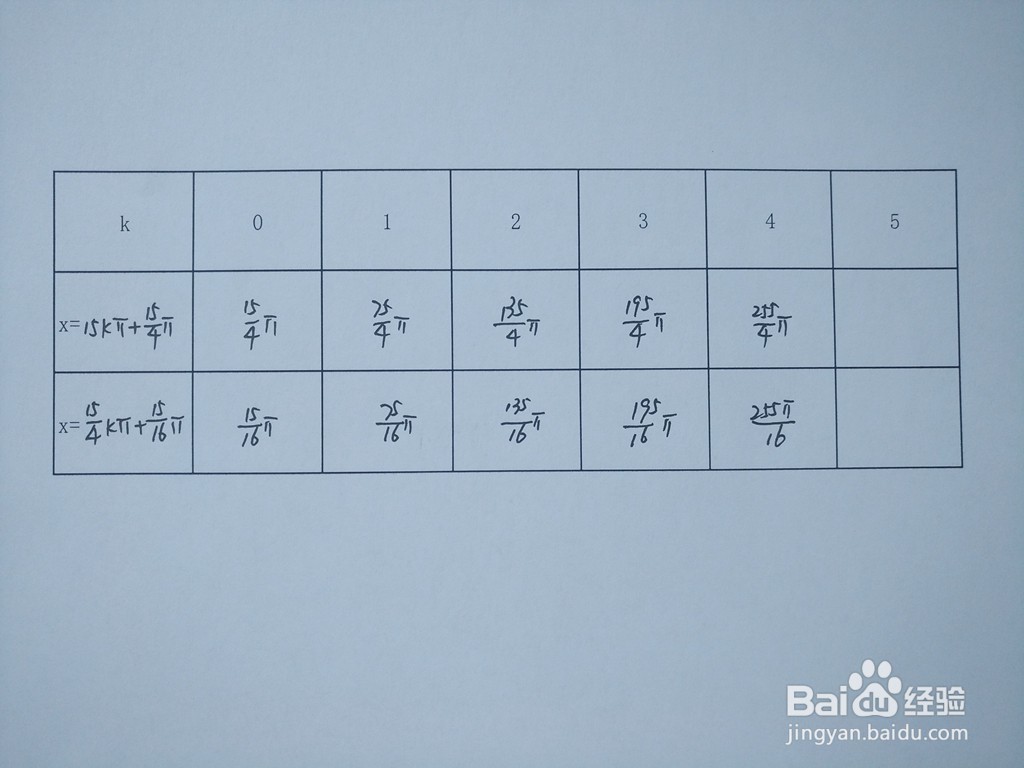
4.函数交点

1、两函数在部分周期内，交点坐标如下：

2、对于正弦函数y=sin x，自变量x只要并且至少增加到x+2π时，函数值才能重复取得。正弦函数和余弦函数的最小正周期是2π。